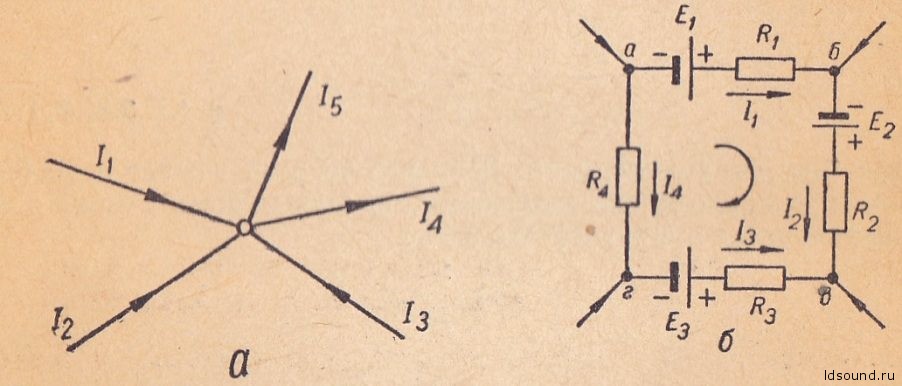
Первый закон. Сумма токов, приходящих к узловой точке (рис. а) равна сумме токов, уходящих от нее:
I1 + I2 + I3 = I4 + I5
Если условно считать токи, приходящие к узловой точке, положительными, а уходящие отрицательными, то первый закон Кирхгофа можно сформулировать так: алгебраическая сумма токов в узловой точке равна нулю:
∑I = 0
Второй закон. Во всяком замкнутом контуре (рис. б) алгебраическая сумма э.д.с. равна алгебраической сумме падения напряжений:
∑E = ∑IR
При произвольно выбранном направлении обхода контура э.д.с. считаются положительными, если их направления совпадают с направлением обхода контура, и отрицательными – если не совпадают. Аналогично падения напряжений считаются положительными, если направление тока в сопротивлениях совпадает с направлением обхода контура, и отрицательным – если не совпадает. Так, для контура абвг (рис. б) при обходе его по часовой стрелке можем написать:
E1 + E2 – E3 = I1R1 + I2R2 – I3R3 – I4R4
На рис. б не показаны внутренние сопротивления r0 источников энергии. Они учтены путем соответствующего увеличения сопротивлений R1, R2 и R3.