Трансмиссионная линия. Что скажет товарищ Kinsler? Часть 3

Ниже приведен близкий к оригиналу перевод главы §10.6 из «Fundamentals Of Acoustics – Fourth Edition (Lawrence E. Kinsler) 2000 ©». Конечно, для лучшего понимания желательно ознакомиться со всем разделом 10 «Трубы, резонаторы и фильтры», а еще лучше – со всей книгой.

§ 10.6 Процессы в комбинированной системе труба-драйвер

В предыдущих главах мы рассмотрели резонансные характеристики трубы. Более реалистичное исследование резонансных свойств должно учитывать свойства механического драйвера, приводимого внешней силой. Драйвер имеет свой собственный механический импеданс. Таким образом, при приложении внешней силы к комбинированной системе драйвер-труба ее механические резонансы будут определяться механическими резонансными характеристиками каждой из ее составляющих – драйвера и трубы.

Для примера, давайте представим драйвер в виде демпфированной колебательной системы как показано на рис. 10.6.1., возбуждаемой внешней колебательной силой f=Fexp(jwt).

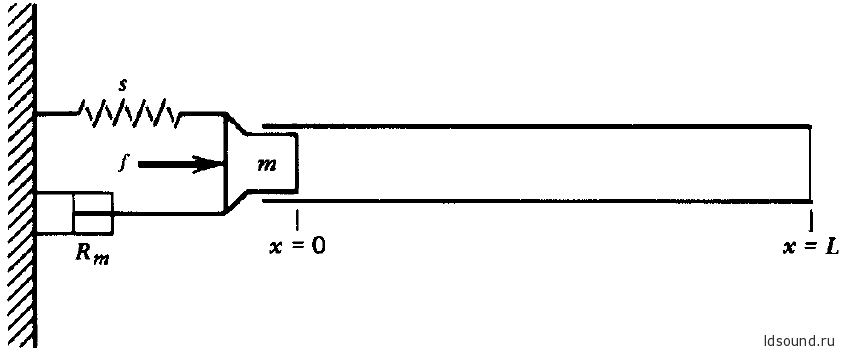
Рис. 10.6.1 Схематическое представление системы драйвер-труба. Труба длиной L, с драйвером, установленным в точке х=0 в виде простого осциллятора массой m, механическим сопротивлением Rm и упругостью (жесткостью) s.

Согласно 2-му закону Ньютона движение массы определяется выражением:

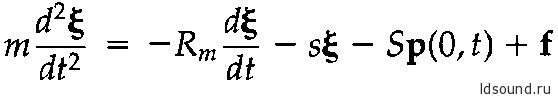
Собственно, это представление F=ma, где F – сумма сил, действующих на динамик, – вся правая часть уравнения. Где ξ – величина смещения массы вправо по трубе и р(0,t) –давление в трубе в точке х=0.

Комплексная скорость массы определяется как u(0,t)=dξ /dt и равна колебательной скорости воздуха в трубе в точке х=0, таким образом выражение (10.6.1) приобретает вид:

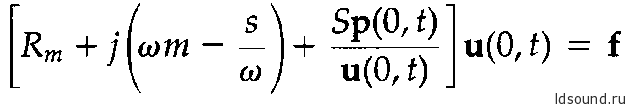
Тут, скорее всего, опущены преобразования, которые были приведены ранее в главе об основах мех.колебаний – см. §1.6, 1.7., где смещение ξ записывается как =exp(jwt) первая/вторая производные записываются как jw exp(jwt) / w² exp(jwt).

Входное механическое сопротивление драйвера Zmd:

Zmd = Rm + j (wm – s/w) (10.6.3)

И, соответственно, входное механическое сопротивление трубы:

Zm0 = (0,) / (0,) (10.6.4)

Таким образом, выражение (10.6.2) показывает, что входное механическое сопротивление Zm рассматриваемой системы драйвер-труба представляет собой комбинацию сопротивлений Zmd и Zm0:

f = Zmu u(O, t) = (Zmd + Zmo) u(O, t) (10.6.5)

Драйвер (без трубы) будет резонировать, когда его реактивное сопротивление стремится к нулю – т.е. на частоте w0=√(s/m). В свою очередь, резонанс трубы (без динамика) будет на частоте, где Im {Zm0}=0. Когда мы имеем дело с комбинацией труба+драйвер для прикладываемой силы входное сопротивление будет представлять сумму сопротивлений трубы и драйвера, таким образом, что частота механического резонанса системы будет определяться из:

Im {Zmd + Zm0} = 0 (10.6.6)

Предположим, что система труба+драйвер имеет жесткую заглушку на конце в точке x=L.

Используя выражение (10.6.3) и выражение (входное удельное сопротивление для трубы с «заглушкой» на конце с потерями- выведено ранее в главе §10.5):

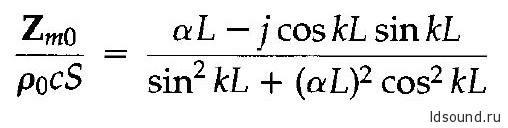
Получаем выражение (10.6.6) в виде:

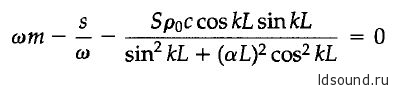
Далее используя выражение для волнового числа k= w/c и обозначив как a = m/Sρ₀L и b = sL/Sρ₀ c² получаем:

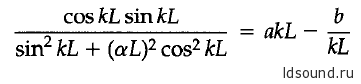
Обратим внимание, что а – отношение массы динамика к массе воздуха, заключенного в объеме трубы и b – отношение упругости подвеса динамика к упругости воздуха в трубе.

Построение графиков для обеих половин выражения (10.6.8) в координатах kL на одной и той же координатной плоскости дает возможность определить частоты механического резонанса в значениях kL как точки их пересечения.

Два примера приведены на рисунке 10.6.2. Примеры иллюстрируют эффекты при применении двух раличных по характеристикам драйверов. (При этом принято, что наша система с малыми потерями и αL≪1, следовательно, реактивное сопротивление трубы – левая половина выражения (10.6.8), пропорционально cotkL – см. §10.5, стр. 277-278).

1. Для легкого и гибкого (с малой жесткостью) динамика с малыми значениями a и b проявляется тенденция к пересечению в точках k_n L ~ (2n-1)π/2, т.е. на расстояниях L~ (2n-1)λ/4 (график 10.6.2а). И при этом в точке х=0 наблюдается практически узел давления.
2. Для «тяжелого» и жесткого динамика график 10.6.2b показывает, что большинство резонансов происходит в точках k_n L ~ nπ, при практически пучности давления в точке х=0. Однако в близи резонанса динамика при k L=3.6π на графике 10.6.2b резонансы системы стремятся к значениям kn L, соответствующим узлу давления в точке х=0.

Поскольку в точке х=L будет всегда пучность давления (тут у нас «жесткая» стенка), если мы сможем выразить амплитуду давления в этой точке через приложенную силу и механическое сопротивление, мы сможем определить зависимость амплитуды в пучности как функцию частоты.

Из выражения (10.5.1):

мы имеем:

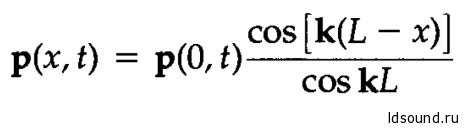
Вычисление этого выражения для точки х=L с учетом (10.6.4) и (10.6.5) приводит к результату:

Для αL≪1 амплитуда давления на жестком конце P(L) составит:

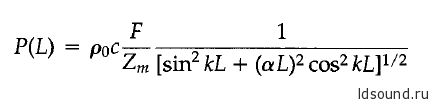
На рисунке 10.6.3 отображены графики амплитуды давления на жестком конце для тех же драйверов, что и в примерах выше, иллюстрированных графиками 10.6.2.

Система с легким и гибким дайвером имеет резонансы с почти постоянным шагом по частоте и почти равными амплитудами давления. (2) Система с тяжелым и жестким драйвером имеет резонансы намного ярче выраженные вблизи собственного резонанса динамика. Кроме того, резонанс драйвера добавляет «экстра» резонанс между k L=3π и k L=4π. Наконец, обратим внимание, что для достаточно больших значений b кривые на графике 10.6.2b могут вообще не пересекаться вблизи и k L=π. Даже если бы это не было истинным резонансом системы в соответствии с нашим определением, т.к. реактивное сопротивление системы не исчезает, существовал бы относительный минимум в реактивном сопротивлении таким образом, что отклик P(L) системы труба-драйвер имел бы пик на этой частоте.

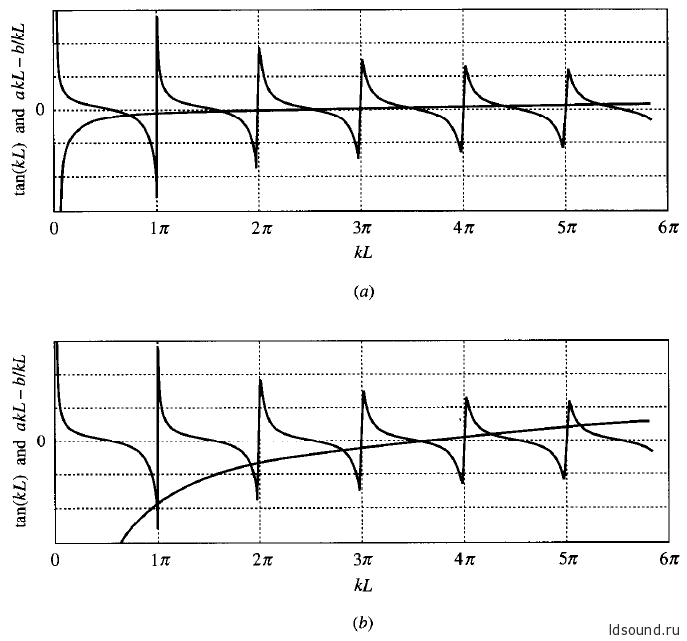
Рис. 10.6.2 Графическое решение для резонансной системы – труба с закрытым жестким концом длиной 1 м и динамиком радиусом 1 см: (а) легким и мягким с а=0,04 и b=2,57; и (b) тяжелым и жестким с а=0,25 и b=32 (тут в обозначении оси ординат, по-видимому, закралась ошибка/опечатка: первые графики- это графики котангенса cot(kL).

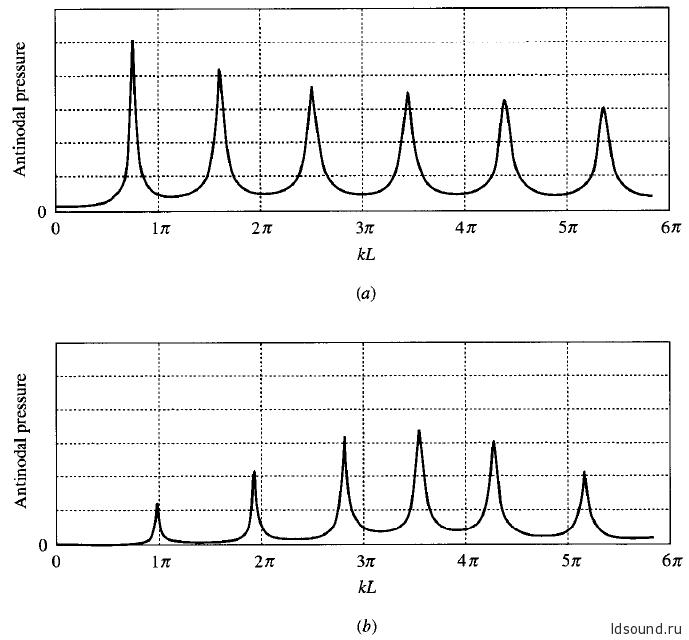
Рис. 10.6.3 Графики амплитуды пучности давления для резонансной системы труба с закрытым жестким концом-драйвер при постоянстве приложенной силы: (а)-легкий и мягкий драйвер (см. рис. 10.6.2а) и (b)- тяжелый и жесткий драйвер (соответственно, рис. 10.6.2b)

Такое взаимодействие динамика (или некого драйвера-источника, излучателя звука в общем случае) при определении резонансов системы заметно проявляется во многих музыкальных инструментах. При игре на духовых инструментах, например, музыкант меняя embouchure (напряжение, положение губ и языка) меняет реактивное сопротивление своего «излучателя» и, следовательно, резонансное сопротивление всей системы. Таким образом, музыкант может «губить» (задавливать) желаемую ноту в пределах полу-тона от соответствующей резонансной частоты инструмента. В равномерно темперированной шкале две соседние частоты- высоты звука отличаются друг от друга на пол-тона, что соответствует f2/f1=2^1/12.

Конец главы 10.6