То, что может показаться на первый взгляд простым, у некоторых людей вызывает недопонимание. Как, например, из круглого фазоинвертора сделать такой же по площади, но прямоугольный, квадратный, треугольный и т.п.? Начинаешь вспоминать геометрию.
Чтобы не путаться и всегда было шпаргалкой, написана данная статья. Переведем из круглой плоскости в другие произвольные плоскости, которыми может обладать фазоинвертор, с сохранением площади. Плоскость это разрез фазоинвертора, для трубы (цилиндра) она имеет форму круга. Наш фазоинвертор в примере ниже имеет постоянную площадь в разрезе, т.е. это не подойдет для конусных ФИ.
Запасайтесь листом и ручкой, так как расчет я буду делать вручную, но никто не запрещает пользоваться онлайн калькулятором для данных вычислений (к примеру вот здесь). Расчет различных площадей будет исходить и ранее известной площади круглого фазоинвертора (трубы). Точные размеры придется подбирать под свою площадь самостоятельно. Для примера я буду подбирать различные площади с фазоинвертора диаметром 10 см.
Площадь круга
Площадь круга: S = ∏ ∙ r2
Пример: S = 3,14 ∙ 52 = 78,5 см2
Полукруг
Площадь полукруга: S = (∏ ∙ r2) / 2
Найдем радиус круга через площадь: r = √ (S / ∏)
Пример: r = √ (78,5 / 3,14) = 5 см
Проверяем: S = 3,14 ∙ 52 = 78,5 см2
Щелевой (прямоугольный или квадратный) фазоинвертор
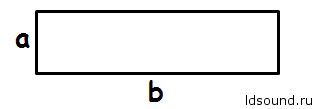
Площадь прямоугольника (квадрата): S = a ∙ b
Для щелевого фазоинвертора я возьму соотношение сторон примерно 1 к 12.
Получается: S = 2,5 ∙ 31,4 = 78,5 см2
Ромб
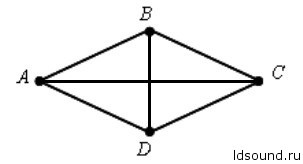
Площадь ромба: S = (AC ∙ BD) / 2
Вычисляем другую диагональ BD через площадь и диагональ AC: BD = 2 ∙ S / AC
Пример: дадим диагонали АС 15 см, тогда BD = 2 ∙ 78,5 / 15 ≈10,4666 см
Проверяем: S = 15 ∙ 10,4666 / 2 = 78,4995 см2
Треугольник

Площадь треугольника: S = ½ ∙ AC ∙ h (половина произведения длины стороны треугольника на длину проведенной к этой стороне высоты). Треугольник может быть как правильным, так и неправильным, но правильный легче считать и строить. Хотя для неправильного треугольника данная формула так же актуальна.
При условии наш треугольник правильный (все стороны равны между собой, а все углы равны 60°), пусть высота h = 11 см, тогда любая из сторон, но в данном случае AC, будет: АС = 2S / h
Пример: AC = 2 ∙ 78,5 / 11 = 14,2727 см
Проверяем: S = ½ ∙ 14,2727 ∙ 11 = 78,4998 см2
Трапеция
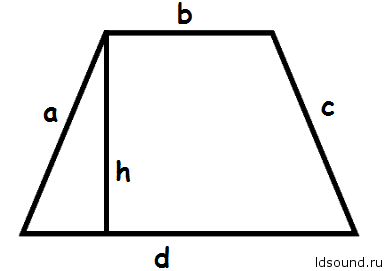
Площадь равнобедренной трапеции: S = ((b + d) / 2) ∙ h
Пример: Будем подбирать трапецию через нашу известную площадь, заданную высоту и верхнюю сторону. Пусть h, высота моей трапеции, будет 3 см, а сторона b = 20 см, тогда основа:
Т.е., основа моей трапеции равна 32,33 см. Как видете расчет не самый простой, по этому советую воспользоватся онлайн калькулятором, ссылка на который приведена выше. По онлайн калькулятору у меня получилась основа 32,34 см.
Параллелограмм
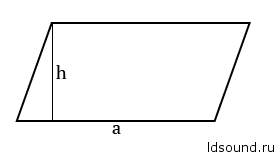
Площадь параллелограмма: S=ah
Пример: пусть высота будет 3 см, тогда сторона a = 78,5 : 3 ≈ 26,17 см
Проверяем: S = 3 ∙ 26,17 = 78,51 см2
Правильный пятиугольник
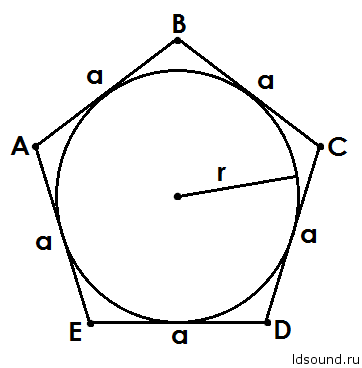
Площадь правильного пятиугольника: S = r ∙ n ∙ a/2, где
n – число сторон;
r – радиус вписанной окружности;
a – одна из сторон пятиугольника.
С пятиугольником уже сложнее подобрать площадь вручную, так как из известных значений у нас только число сторон n. По этому советую воспользоваться онлайн калькулятором. На вскидку скажу, что в моем варианте сторона a = 6,64 см, при таком значении площадь составляет 75,85 см2.
Правильный шестиугольник
С шестиугольником точно так же как и с пятиугольником, по этому разбирать сложные расчеты не стану – онлайн калькулятор в помощь.
Эллипс
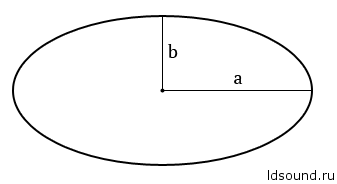
Площадь эллипса равна произведению ∏ на большую полуось и малую полуось: S=∏ab
Большая полуось a должна быть ровно в два раза больше малой полуоси b. Если кому хочется рассчитать вручную, то пожалуйста мой пример ниже.
Пример: подбор площади будет происходить через известное число ∏ и требуемую площадь, в моем случае 78,5 см2.
78,5 = 3,14 ∙ 2х ∙ х
78,5 = 3,14 ∙ 2х2
78,5 = 6,28 ∙ х2
х2 = 78,5 : 6,28 = 12,5
х = √12,5 ≈ 3,53
Проверяем: 3,14 ∙ 3,53 ∙ 7,06 = 78,25 см2
В заключении. Площадь таких фигур как звезда или загогулины приводить не буду, это уж слишком большое извращение. Но никто не запрещает разделить звезду на 5 треугольников и один пятиугольник и как то подсчитать все это.
Так же не забывайте, что есть еще фазоинверторы с расширением к выходу наружу. Такие формы позволяют убрать «свист» в трубе и уменьшить его длину. Но мой пример к этому не относится.
По своему опыту скажу, что труба проще в изготовлении, а иногда и доступность в наличии, но по показателю свиста и сложности изготовления я бы использовал щелевой (прямоугольный) фазоинвертор.

