С.Н. Зотов
В статье сделан обзор способов расчёта резонансной частоты фазоинвертора (резонатора Гельмгольца) для различных конструкций, включая туннели с переменным сечением и варианты конструкций с несколькими произвольными туннелями.
1. ВВЕДЕНИЕ
Многие считают, что в расчёте фазоинвертора (ФИ) нет ничего сложного, и отчасти будут правы – ведь в книгах и справочниках для радиолюбителей по проектированию акустических систем приводятся соответствующие формулы для расчёта частоты резонанса ФИ.
Однако, в данной статье будут рассмотрены и ″сложные″ случаи конструкций фазоинверторов, а именно – для туннелей с переменным сечением и для случаев с применением нескольких разных туннелей; и как в таком случае рассчитывать резонанс(?..)
Сейчас в Интернете можно найти различные расчётные программы-симуляторы, и по ним выполнить практически любые вычисления; однако, так и не поняв, ″как это считается″. Так что, данная статья будет полезной, в первую очередь, тем разработчикам и конструкторам акустических систем, кто желает делать математические расчёты самостоятельно по формулам.
Сразу оговоримся, что статья посвящена именно методикам расчёта частоты резонанса туннеля в зависимости от геометрических размеров туннеля.
В статье не рассматриваются проблемы с определением так называемой ″оптимальной″ частоты настройки фазоинвертора, т.е. такой его частоты резонанса, при которой амплитудно-частотная характеристика громкоговорителя в области низких частот получается максимально гладкой. Это совершенно другая задача – поиска оптимальной частоты fb в зависимости от соотношения ТС-параметров громкоговорителя и объёма ящика.
2. КАК ИЗМЕРИТЬ РЕЗОНАНС ФАЗОИНВЕРТОРА
Упрощённо можно представить подвижную систему громкоговорителя как некий маятник типа ″груз на пружине″, где груз маятника – это масса подвижной системы динамика, а пружина – это упругий подвес.
Поэтому громкоговоритель (или по-простому – динамик) аналогично маятнику имеет в свободном пространстве отчётливо выраженный резонанс; похожий резонанс наблюдается, если динамик разместить в закрытом ящике.
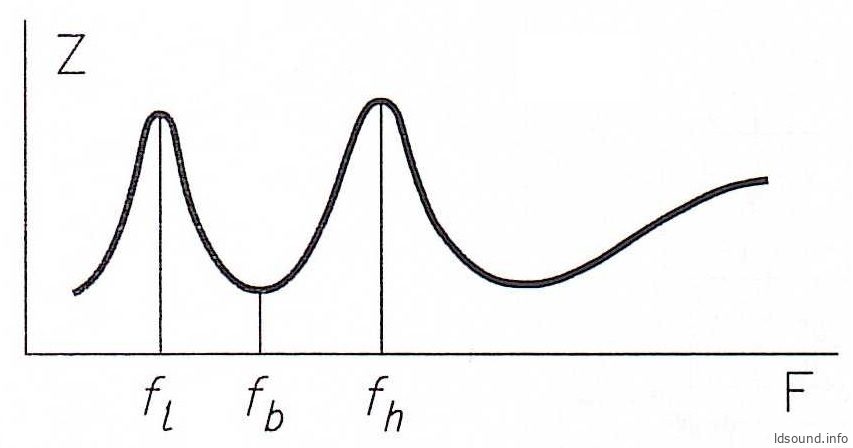
Однако же, если динамик установить в ящике с фазоинвертором, то на кривой импеданса будет наблюдаться два пика (на частотах fl и fh); амплитуды и частоты этих пиков – в общем случае зависят от комбинации ТС-параметров громкоговорителя и оформления (например, при увеличении объёма ящика V эти два пика приближаются друг к другу, а при уменьшении объёма V эти пики удаляются друг от друга – см. Эфрусси [1]). Но при этом провал между двумя пиками всегда будет точно соответствовать частоте резонанса фазоинвертора fb, см. рис. 1.
В конечном счёте, измерить частоту резонанса ФИ не составляет особого труда; нужно только иметь звуковой генератор и тестер, ну и ещё правильно собрать простейшую схему…
Рис. 1. Частотная характеристика модуля полного сопротивления громкоговорителя в ящике с фазоинвертором:
Иногда в фазоинверсных акустических системах применяют две одинаковые трубы (вместо одной трубы большего диаметра). И, в принципе, хорошо известно, как такой ФИ рассчитывается.
Но создадим интригу!.. Что будет, если в ящике с ФИ установить две разные трубы? Т.е. эти две трубы могут быть: одного диаметра, но с разной длиной; или одинаковой длины, но с разными диаметрами; или же в общем случае – одновременно с разными и диаметрами и длиной.
И что будет в итоге? На кривой импеданса – будет два резонанса ФИ, или же всё-таки будет один резонанс fb (?)
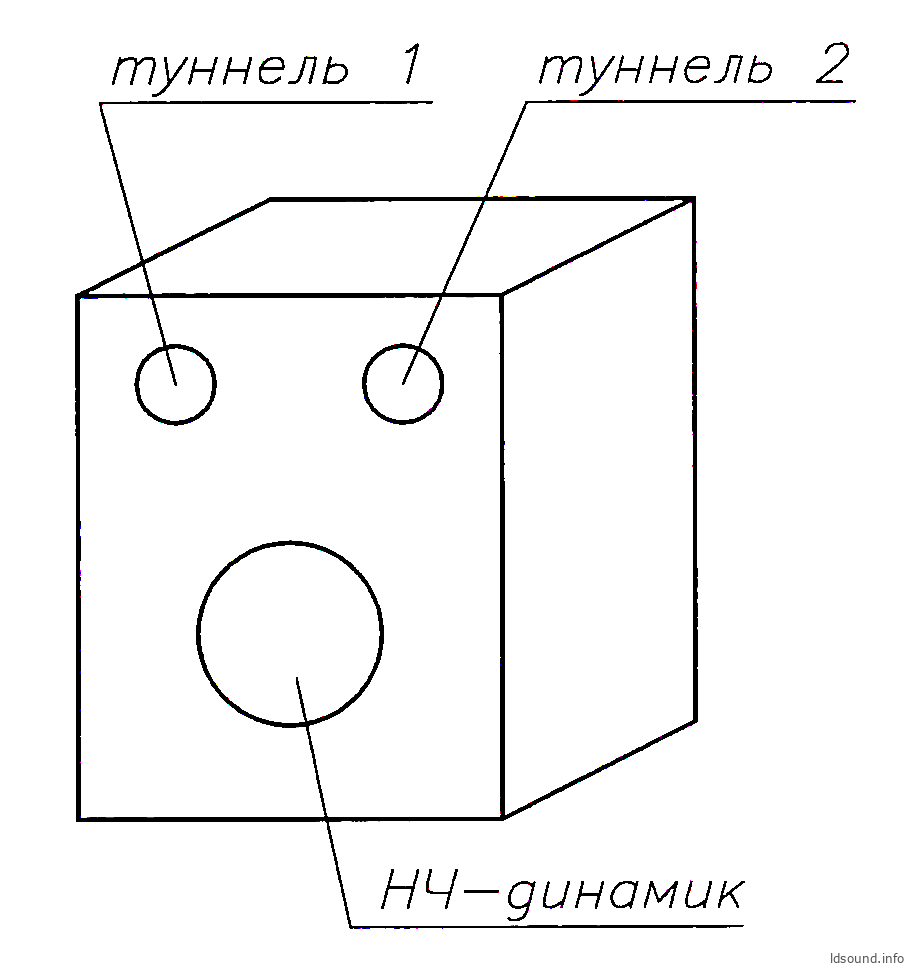
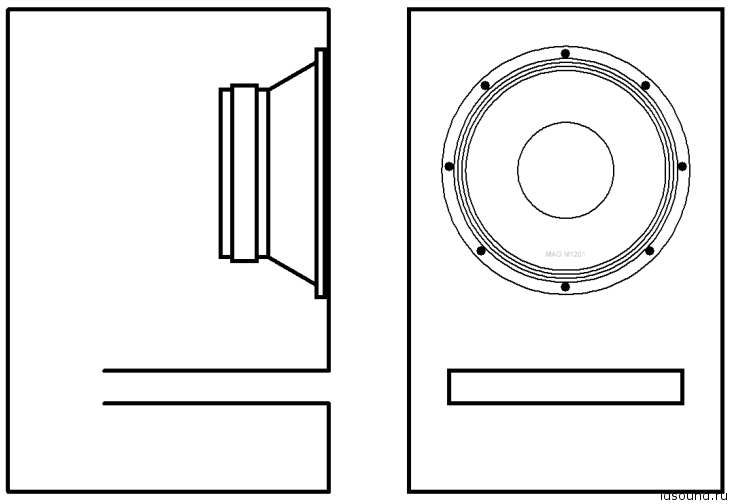
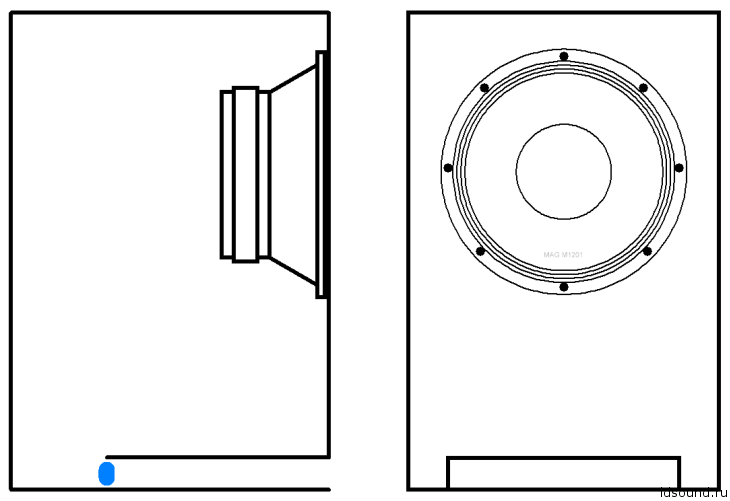
Был проведён интересный эксперимент: в ящике объёмом V=31 л были установлены два круглых туннеля с одинаковым диаметром, но с разной длиной, см. рис. 2 (с трубами одинакового диаметра оказалось проще выполнять столярные работы). Геометрические размеры туннелей:
- туннель № 1 – диаметр D1=51,3 мм, длина L1=90 мм;
- туннель № 2 – диаметр D2=51,3 мм, длина L2=157 мм.
В ходе измерений выяснилось, что резонанс фазоинвертора – только один (!), и в данном конкретном случае этот резонанс составил fb=50,0 Гц. Интрига состоит в том, что далее в статье будет показано, как такой фазоинвертор рассчитывается…
Рис. 2. Эксперимент: ящик объёмом V=31 л, с двумя разными туннелями, пояснения в тексте:
Для лучшего понимания начинать обзор способов расчёта резонанса фазоинвертора следует с простейших случаев, постепенно усложняя конструкции.
3. ТУННЕЛЬ – ЦИЛИНДРИЧЕСКАЯ ТРУБА
Рассмотрим самый простой случай фазоинвертора – одинокий туннель с постоянным сечением. В известной книге Виноградовой [2] приводится общая формула взаимосвязи геометрических размеров туннеля фазоинвертора с его резонансной частотой:
L / S = 3097 / (fb2 · V) (1)
где:
- L [м] – длина туннеля ФИ;
- S [м2] – площадь сечения туннеля ФИ;
- V [м3] – объём ящика;
- fb [Гц] – частота резонанса ФИ.
В книге Виноградовой отмечено также, что в приведённой формуле ″L″ – это кажущаяся длина туннеля, включающая как непосредственно геометрическую длину туннеля, так и приращение за счёт так называемых ″краевых эффектов″.
Числовой коэффициент ″3097″ включает в себя скорость звука в воздухе при нормальных условиях и число ″2π″, а также зависит от размерностей используемых в формуле параметров.
Из этой формулы следует, что резонансная частота фазоинвертора в квадрате пропорциональна отношению площади туннеля к его длине:
fb2 ∼ S / L
или если убрать вторую степень при частоте – резонансная частота ФИ пропорциональна корню квадратному из этого отношения:
fb ∼ √ (S / L) (2)
При использовании в качестве туннеля ФИ цилиндрической трубы целесообразно формулу (1) преобразовать к более удобному виду:
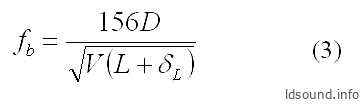
где:
- fb [Гц] – резонанс ФИ;
- D [см] – диаметр трубы ФИ (имеется в виду внутренний диаметр трубы);
- V [л] – объём ящика;
- L [см] – длина трубы;
- δL [см] – поправка на краевой эффект трубы.
Виноградова указывает, как рассчитывается эта поправка:
δL = 1,7 · √ (S / π) (4)
для случая круглой трубы поправку можно выразить через диаметр:
δL = 0,85D (5)
Для наглядности – покажем на конкретных примерах, как рассчитывается ФИ…
ПРИМЕР 1:
Ящик объёмом V=60 л, фазоинвертор представляет собой одну круглую трубу диаметром D=7 см, длина трубы L=20 см. Рассчитаем резонансную частоту ФИ:
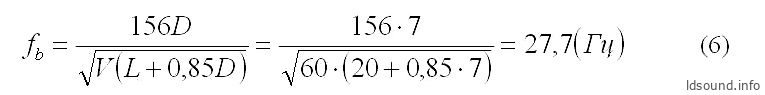
Следует отметить, что краевой эффект трубы в данном случае составляет:
δL = 0,85D = 0,85 · 7 = 5,95 ≈ 6 (см)
т.е. труба ″виртуально″ увеличивается на δL≈6 см, что и приводит к некоторому снижению резонанса.
И сразу – ещё один пример…
ПРИМЕР 2:
Тот же ящик объёмом V=60 л, но фазоинвертор представляет собой две круглые трубы такого же размера, т.е. диаметром D=7 см и длиной L=20 см. Как изменится резонансная частота?
В этом случае суммарное сечение труб увеличится в 2 раза, а длина труб останется прежней – и, согласно формуле (2), это приведёт к повышению резонансной частоты ФИ в КОРЕНЬ ИЗ ДВУХ РАЗ, т.е. в 1,41 раза; таким образом, резонансная частота станет:
fb = 1,41 * 27,7 = 39,1 Гц (7)
Если установить три одинаковые трубы, то резонансная частота увеличится в КОРЕНЬ ИЗ ТРЁХ РАЗ, т.е. в 1,73 раза (по тем же соображениям); а в общем случае резонанс увеличивается в КОРЕНЬ ИЗ ″N ″ РАЗ, где ″N ″ – количество труб (с одной оговоркой – трубы должны быть одинаковые).
В случае использования цилиндрического туннеля формула (3) обеспечивает (согласно статистическим данным) малую погрешность, что даёт возможность по частоте резонанса фазоинвертора довольно точно определить объём ящика V. Иногда это бывает необходимо; например, когда не удаётся точно рассчитать вытесненные (магнитными системами динамиков, распорками, фильтрами и т.п.) объёмы ящика. Кроме этого, применение звукопоглощающего материала приводит к увеличению ″эффективного″ объёма ящика.
Поэтому, если известны геометрические размеры цилиндрического туннеля и экспериментальным путём измерена частота резонанса ФИ, то объём ящика можно уточнить следующим образом:
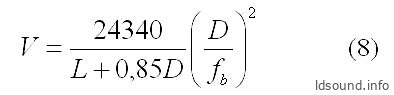
где:
- V [л] – объём ящика;
- L [см] – длина трубы;
- D [см] – диаметр трубы;
- fb [Гц] – измеренный резонанс фазоинвертора.
4. ВЫБОР СЕЧЕНИЯ И ДЛИНЫ ТУННЕЛЯ
Как уже было отмечено выше, из формулы (2) следует, что резонансная частота фазоинвертора определяется отношением площади туннеля к его длине; таким образом, одну и ту же резонансную частоту fb можно получить, применяя туннели разного размера: с небольшим сечением и небольшой длиной или с большим сечением и пропорционально увеличенной длиной.
Однако, уменьшение сечения туннеля приводит к увеличению скорости воздушного потока в туннеле, в результате чего увеличиваются потери и могут появиться посторонние свистящие призвуки в ФИ.
Поэтому предпочтительнее конструировать туннели по возможности с максимально большим сечением; однако, при этом пропорционально увеличивается также и длина туннеля – а это может иметь конструктивные ограничения, т.к. слишком длинный туннель может упираться в заднюю стенку ящика.
В таких случаях иногда применяют изогнутые туннели, что позволяет увеличить сечение туннеля до приемлемой величины и тем самым повысить качество работы ФИ. Например, изогнутый туннель используется в промышленной акустической системе типа «35АС-1» рижского радиозавода, см. рис. 3.
Расчёт резонансной частоты изогнутых туннелей осуществляется по тем же формулам что и для прямых туннелей; и, согласно статистике, больших погрешностей при таких расчётах не возникает. Только следует в соответствующих формулах подставлять длину туннеля ″L″, определённую по средней линии туннеля.
Рис. 3. Акустическая система «35АС-1» и изогнутый туннель ФИ от неё.
Если всё-таки не принимать во внимание изогнутые туннели и рассматривать только прямые, то выбор величины сечения туннеля представляет собой непростую задачу. Итальянский инженер-акустик Жан-Пьеро Матараццо предлагает несколько вариантов конструкций туннелей [3], в которых длина туннеля имеет уменьшенную величину по сравнению с традиционными цилиндрическими туннелями при сохранении частоты резонанса (его статья так и называется – «Фазоинвертор: короче!»). Достигается это в основном применением туннелей с переменным сечением (конический туннель, ″песочные часы″, экспоненциальный туннель).
Статья, безусловно, интересная, но всё-таки Матараццо немного слукавил… Потому что представил результаты своего исследования в виде таблиц; однако же, если в проектируемой акустике размеры туннеля не попадают в представленные табличные значения, то затруднительно эту информацию использовать – ведь никаких формул для расчётов этих туннелей не приведено.
Какие же существуют рекомендации по величине сечения туннеля фазоинвертора? Обычно, величину сечения оценивают по отношению площади сечения туннеля ФИ к площади диффузора низкочастотного динамика, т.е. по отношению kФ=SФ/SДИФ; в случаях, когда используется несколько туннелей, а в качестве низкочастотного звена применяется ″групповой излучатель″ (т.е. несколько НЧ-динамиков), то под величиной kФ нужно считать отношение суммарной площади туннелей к суммарной площади диффузоров. Виноградова рекомендует принимать площадь сечения туннеля в интервале kФ=0,25…1,0; Эфрусси – рекомендует принимать kФ=0,25…0,5.
Матараццо в своей статье приводит эмпирическую формулу Р. Смолла, по которой можно рассчитать минимально допустимый диаметр туннеля ФИ:
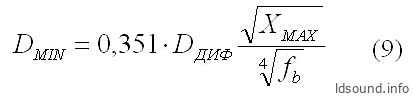
где:
- DMIN [см] – минимально допустимый диаметр туннеля ФИ;
- DДИФ [см] – диаметр диффузора динамика;
- XMAX [см] – максимальное осевое смещение диффузора динамика;
- fb [Гц] – резонанс ФИ.
Иофе и Лизунков [4] предлагают задавать потери в туннеле фазоинвертора, и показывают, как именно рассчитать диаметр туннеля с учётом этих потерь; величина потерь туннеля задаётся безразмерным параметром – добротностью фазоинвертора QФ. Для желающих ознакомиться с этой методикой – ссылка приводится в конце статьи.
Рекомендации ″по Матараццо″ дают величину сечения туннеля в несколько раз мéньшую, чем ″по Виноградовой-Эфрусси″. И это естественно, т.к. Матараццо показывает минимально допустимый диаметр туннеля, меньше которого уже возникают недопустимые искажения; а у Виноградовой-Эфрусси – предлагается сечение, при котором качество ФИ остаётся достаточно высоким.
Кстати, сечение туннеля в упомянутой выше акустической системе «35АС-1» имеет соотношение площадей около kФ≈0,25.
5. ТУННЕЛЬ С ПРЯМОУГОЛЬНЫМ СЕЧЕНИЕМ
При использовании прямоугольного сечения можно рассчитывать резонанс ФИ через площадь сечения туннеля, используя формулу (1). Но можно также вычислять и по формуле для круглой трубы (3), только предварительно её нужно немного преобразовать. И в итоге резонансная частота для прямоугольной трубы вычисляется почти также:
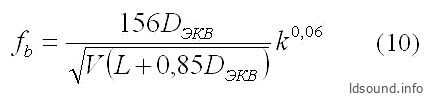
где:
- fb [Гц] – резонанс ФИ;
- DЭКВ [см] – вводится так называемый эквивалентный диаметр трубы ФИ (который рассчитывается как ″круглая труба, равная по сечению прямоугольному туннелю″);
- V [л] – объём ящика;
- L [см] – длина трубы; кроме того, согласно рекомендациям Эфрусси [1], вводится поправка k=(b/a), учитывающая влияние соотношения сторон прямоугольного сечения туннеля (здесь: ″a″ и ″b″ [см] – стороны прямоугольного туннеля, причём b>a, это важно).
Эквивалентный диаметр для прямоугольного сечения, по определению, равен:
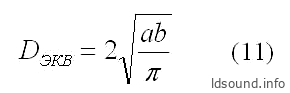
Из приведённых формул следует, что прямоугольный туннель (равного сечения и длины) обеспечивает немного более высокую частоту резонанса по сравнению с круглой трубой. Величина повышения частоты резонанса зависит от отношения сторон прямоугольного туннеля: например, при отношении сторон (b/a)=3 – повышение частоты резонанса составляет около +7%; при большом отношении, как у щелевых туннелей – fb повышается сильнее, например, для (b/a)=15 получается уже около +17%.
Матараццо рекомендует щелевой туннель располагать вблизи стенки ящика, т.к. это увеличивает виртуальную длину туннеля за счёт дополнительного краевого эффекта (примерно на 15%) по сравнению с аналогичным туннелем, расположенным далеко от стенки ящика, см. рис. 4.
Рис. 4. Рисунки, скопированные из статьи Матараццо:
Экспериментальным путём можно довольно точно установить величину виртуального удлинения туннеля за счёт краевого эффекта, если известны геометрические размеры туннеля, объём ящика и измерена резонансная частота ФИ; расчёт выполняется следующим образом:
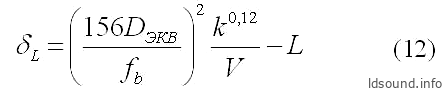
где:
- δL [см] – поправка на краевой эффект;
- DЭКВ [см] – эквивалентный диаметр туннеля;
- fb [Гц] – измеренный резонанс ФИ;
- k=(b/a), здесь ″a″ и ″b″ – стороны прямоугольного туннеля, b>a);
- V [л] – объём ящика;
- L [см] – геометрическая длина туннеля.
Предложенный способ определения экспериментальным путём величины виртуального удлинения туннеля за счёт краевого эффекта можно применять не только для щелевого туннеля, но в общем случае и для туннелей с иными конструкциями.
6. РАСЧЁТЫ ФАЗОИНВЕРТОРА ЧЕРЕЗ ПРОВОДИМОСТИ
Оказывается, если при расчётах фазоинвертора ″оперировать″ так называемыми проводимостями туннеля, то становится возможным довольно легко выполнять расчёты для сложных конструкций туннелей (в т.ч. туннелей с переменным сечением или конструкций с несколькими произвольными туннелями).
6.1. И.Б. КРЕНДАЛЛ
Как-то случайно зашёл в книжный магазин, где в букинистическом отделе увидел и купил очень древнюю книгу по акустике [5]; её автор И.Б. Крендалл (Irwing B. Crandall) инженер-акустик, работавший в начале 20-го века в телефонной лаборатории А. Белла. Книга была издана в Нью-Йорке в 1927 году, а в 1934 году переиздана в русском переводе.
В этой книге кроме прочего оказался и раздел о резонаторах Гельмгольца, где расчёты предлагалось вести через проводимости туннеля, что позволяет решать задачу в общем виде и довольно легко. Вот интересная цитата из книги:
«Представление о проводимости, помимо того, что ведет к простой формуле для собственной частоты, облегчает определение полной проводимости в случае, когда две или более проводимости соединены последовательно или параллельно; формулы идентичны с теми, помощью которых вычисляют электрические проводимости…»
В итоге, перечитав эту главу несколько раз, я понял, как рассчитывать туннели с переменным сечением…
Рис. 5. Фрагменты из книги Крендалла:
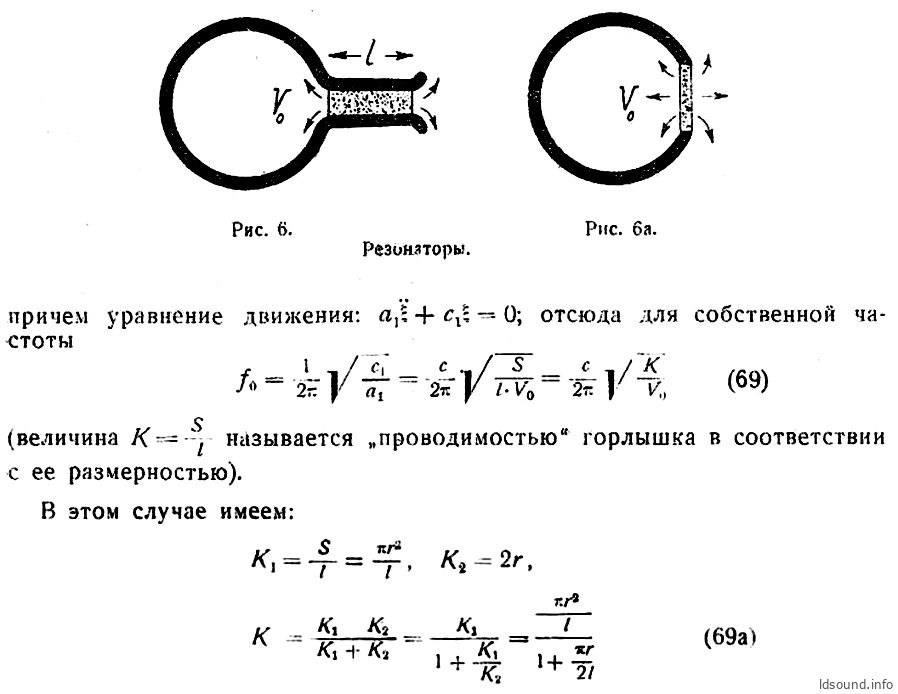
6.2. РАСЧЁТ ЦИЛИНДРИЧЕСКОЙ ТРУБЫ ЧЕРЕЗ ПРОВОДИМОСТИ
Для расчёта фазоинвертора через проводимости можно воспользоваться формулой из книги Крендалла, но можно также и преобразовать формулу (1) к нужному виду:
fb = 176 √ (K0/V) (13)
где:
- fb [Гц] – частота резонанса ФИ;
- К0 [см] – общая проводимость туннеля;
- V [л] – объём ящика.
Общая проводимость цилиндрического туннеля ″по Крендаллу″ получается последовательным соединением двух проводимостей: проводимости непосредственно туннеля К1 и проводимости ″круглого отверстия в тонкой стенке″ К2 , которые равны:
K1 = S / L = 4D2/ 4L (14)
K2 = D (15)
Но вычисляется общая проводимость туннеля при последовательном соединении проводимостей – путём сложения величин, обратных проводимостям (точно так же, как и при расчёте общего сопротивления при параллельном соединении резисторов):
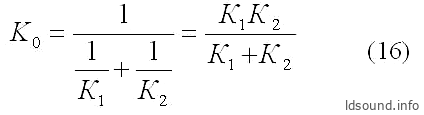
где:
- К1 [см] – проводимость собственно цилиндрического туннеля;
- К2 [см] – проводимость круглого отверстия в тонкой стенке;
- К0 [см] – общая проводимость туннеля;
- S [см2] – площадь сечения туннеля;
- D [см] – диаметр туннеля;
- L [см] – длина туннеля.
Аналогично для наглядности покажем на конкретных примерах, как резонанс фазоинвертора вычисляется, но уже через проводимости.
ПРИМЕР 3. Ящик объёмом V=60 л, фазоинвертор представляет собой одну круглую трубу диаметром D=7 см, длина трубы L=20 см; этот пример ранее уже фигурировал, но теперь повторно решим его же, оперируя на этот раз проводимостями. Сначала определим общую проводимость туннеля:
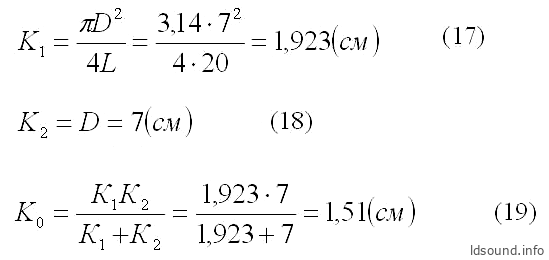
Далее по формуле (13) рассчитаем резонанс ФИ:
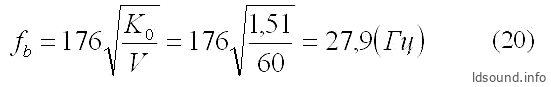
Итак, расчёты ″по Крендаллу″ показали fb=27,9 Гц, а ″по Виноградовой″ – fb=27,7 Гц, расхождение результатов всего 0,2 Гц (!)
Можно отметить, что в формуле расчёта резонанса ″по Крендаллу″ (13) отсутствует поправка на краевой эффект δL , т.к. эта поправка уже была учтена проводимостью отверстия в тонкой стенке К2 (!)
Если общая проводимость туннеля при последовательном соединении проводимостей вычисляется через сложение величин, обратных проводимостям, то при параллельном соединении проводимостей – проводимости просто складываются арифметически.
ПРИМЕР 4. Тот же ящик объёмом V=60 л, но фазоинвертор представляет собой две круглые трубы такого же размера, т.е. диаметром D=7 см и длиной L=20 см. Как изменится резонансная частота? Этот пример также ранее уже приводился, но по аналогии решим задачу через проводимости.
Общая проводимость одиночного круглого туннеля с размерами D=7 см и L=20 см уже была определена ранее, см. (19), таким образом, К0=1,51(см).
Две одинаковые трубы в ящике – это параллельное соединение проводимостей, при котором суммарная проводимость вычисляется простым сложением, т.е.:
K∑ = K0 + K0 = 1,51 + 1,51 = 3,02 см (21)
И по формуле (13) определяем резонанс ФИ:

Сравнение с (7) показывает похожее по точности совпадение, расхождение между разными расчётными методиками по частоте резонанса fb всего 0,4 Гц.
ПРИМЕР 5. А теперь проверим, как ″работает″ этот математический алгоритм на экспериментальном примере, показанном в начале статьи (рис. 2). Итак, ящик объёмом V=31 л с двумя разными туннелями:
- туннель № 1 – диаметр D1=51,3 мм, длина L1=90 мм;
- туннель № 2 – диаметр D2=51,3 мм, длина L2=157 мм.
Рассчитаем резонансную частоту ″по Крендаллу″. Сначала определим общие проводимости для каждого из туннелей; для первого (короткого) туннеля:
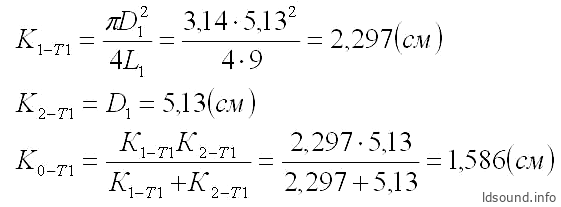
и для второго (длинного) туннеля:
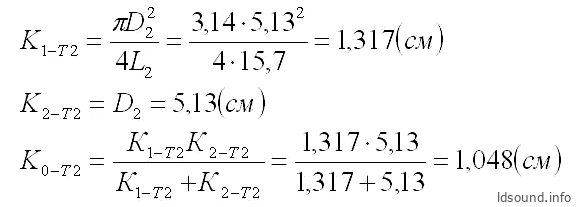
Общая проводимость при параллельном соединении двух разных проводимостей:
K∑ = K0-T1 + K0-T2 = 1,586 + 1,048 = 2,634 см (23)
И, наконец, по формуле (13) определяем резонанс ФИ:
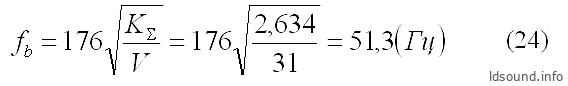
Расчёты частоты резонанса ″по Крендаллу″ дали результат fb=51,3 Гц; в то время как измерение частоты резонанса в экспериментальной колонке показали результат fb=50,0 Гц. Расхождение результатов составило около 2,5% – это немного больше ожидаемого результата, хотя тоже неплохо. Вероятнее всего, при испытаниях были допущены погрешности в определении частоты резонанса; также, возможно, не совсем точно был определён объём ящика.
Но ″подгонять″ результаты не стал…
6.3. РАСЧЁТ КОНИЧЕСКОГО ТУННЕЛЯ
Если быть точным в формулировках, то такой туннель прáвильнее называть туннелем в виде усечённого конуса, но для простоты будем называть его коническим. По утверждению Матараццо [3] – использование конического туннеля позволяет уменьшить диаметр входного отверстия по сравнению с минимально допустимой величиной по формуле Р. Смола (9) без опасности появления посторонних свистящих шумов, т.к. выходное отверстие туннеля на лицевой панели ящика остаётся относительно большим. Такая конструкция позволяет уменьшить длину туннеля при сохранении частоты резонанса.
Итак, конический туннель можно представить как последовательное соединение большого числа проводимостей, что позволяет применить методику, представленную в книге Крендалла.
Задача сводится к вычислению общей проводимости конического туннеля, потому что если проводимость туннеля известна, то дальнейший расчёт резонанса фазоинвертора выполняется элементарно…
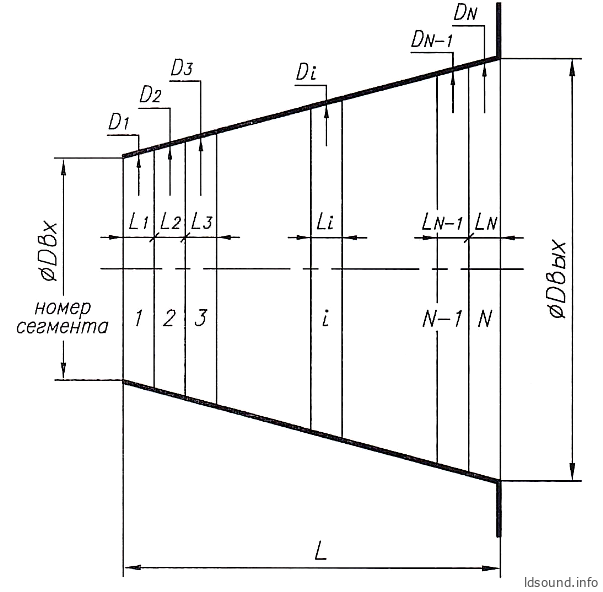
Предположим, геометрические размеры конического туннеля известны, это диаметры входа и выхода, и длина туннеля. Для вычисления его проводимости нужно поделить весь туннель по длине на N одинаковых сегментов, см. рис. 6. Для повышения точности расчётов желательно, чтобы число сегментов было бы большим (например, N ≥ 100 ).
Итак, осевые размеры всех сегментов равны:
L1 = L2 = L3 = … = Li = … = LN-1 = LN = L / N (25)
где:
- L1, L2, L3 … Li … LN [см] – длина сегментов туннеля;
- L [см] – общая длина туннеля, N – заданное количество сегментов туннеля.
Следующим этапом нужно для каждого сегмента определить диаметры, а точнее диаметры по середине каждого из сегментов, т.е.: D1, D2, D3 … DN – это средние диаметры, соответственно 1-го, 2-го, 3-го … N-го сегментов туннеля. Поскольку для конического туннеля закон формирования образующей профиля известен (это – прямая), то определение средних диаметров сегментов представляет собой относительно несложную геометрическую задачу.
Рис. 6. Расчётная схема конического туннеля:
Далее вычисляем проводимости для каждого сегмента:
где:
- К1, К2, К3 … Кi … КN [см] – проводимости сегментов туннеля;
- D1, D2, D3 … Di … … DN [см] – средние диаметры каждого из сегментов;
- L1=L2=L3= … =Li= … =LN [см] – все длины каждого из сегментов равны между собой, и рассчитываются по формуле (25).
И, наконец, вычисляем общую проводимость туннеля:
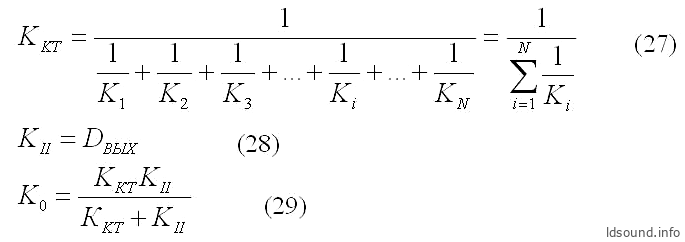
где:
- КKТ [см] – проводимость конического туннеля;
- КII [см] – проводимость отверстия в тонкой стенке;
- К0 [см] – общая проводимость конического туннеля;
- DВЫХ [см] – диаметр выходного отверстия туннеля.
В заключение нужно рассчитать по уже известной формуле (13) резонансную частоту фазоинвертора – и задача с коническим туннелем решена.
Эту же методику можно применить не только к коническим туннелям, но и к любым другим круглым туннелям с переменным сечением при условии, что известен закон формирования ″образующей кривой″ по длине туннеля.
В расчётной схеме конического туннеля (рис. 6) указаны совершенно конкретные размеры – диаметр входа (DВХ), диаметр выхода (DВЫХ) и длина туннеля (L). На практике часто (особенно в случаях, если туннели – покупные из пластика) имеет место закругление выходного отверстия туннеля, см. рис. 7. В подобных ситуациях довольно затруднительно точно указать диаметр выходного отверстия и точную длину туннеля. Именно эти обстоятельства могут приводить к возникновению погрешностей при вычислениях проводимости туннеля, если возникнет желание проверить покупной туннель расчётным путём. Кстати, имеющиеся в продаже готовые трубы ФИ для колонок имеют в паспортных данных сведения только о диаметре и длине труб, но значительно полезнее было бы давать сведения о проводимости готовых туннелей (чего не делается).
Рис. 7. Объяснение возможных погрешностей в расчётах при закруглении выходного отверстия туннеля:
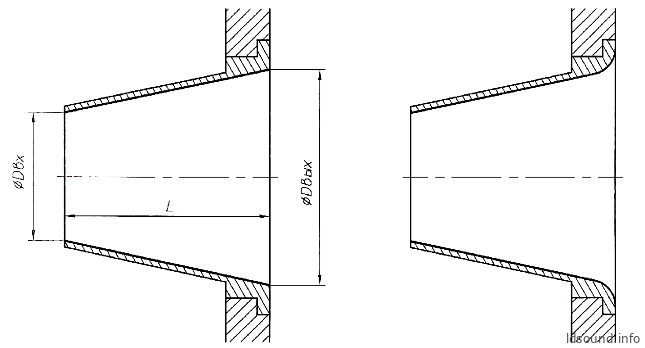
ПРИМЕР 6. ЗАДАНО: объём ящика V=30 л, имеется НЧ-динамик 35ГДН-1-4 (диаметр диффузора DДИФ=14 см, максимальное осевое смещение диффузора XMAX=0,8 см).
ОПРЕДЕЛИТЬ: конструкцию туннеля ФИ с резонансной частотой fb=33 Гц, при условии, что отношение площадей ФИ и диффузора должно быть kФ=0,25, а длина туннеля не должна превышать L=15 см (конструктивное ограничение, чтобы туннель не упирался в заднюю стенку ящика).
1. Определим диаметр трубы ФИ; т.к. задано отношение kФ=(SФ/SДИФ)=0,25, то диаметр туннеля рассчитывается следующим образом:
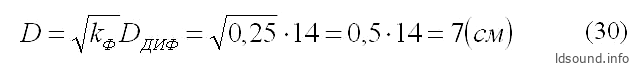
где:
- D [см] – диаметр туннеля ФИ;
- DДИФ [см] – диаметр диффузора;
- kФ – заданный коэффициент отношения площадей туннеля ФИ и диффузора динамика.
2. Проверим сначала возможность применения простой круглой трубы; для расчёта длины цилиндрического туннеля преобразуем формулу (3), и получим:
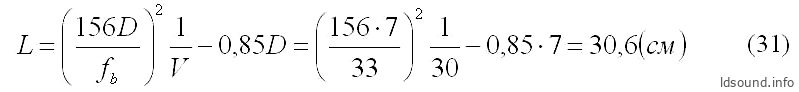
где:
- L [см] – длина цилиндрической трубы;
- D [см] – диаметр туннеля ФИ;
- fb [Гц] – заданный резонанс фазоинвертора;
- V [л] – объём ящика.
3. Предварительный расчёт показал, что цилиндрическая труба не годится, т.к. при заданном диаметре для получения fb=33 Гц её длина должна быть более L≈30 см, что противоречит условию задачи о конструктивном ограничении (нужно не более L=15 см).
Поэтому рассмотрим варианты с коническим туннелем, при этом примем длину туннеля L=15 см, выходной диаметр туннеля DВЫХ=7 см (для получения заданного kФ=0,25); и будем менять только входной диаметр туннеля DВХ до получения требуемого результата.
Изложенный выше математический алгоритм был запрограммирован на компьютере, после чего выполнены расчёты нескольких вариантов с разными геометрическими параметрами конических туннелей; результаты сведены в таблицу.
| Номер расчётного варианта | 1* | 2 | 3 | 4 | 5 | 6 |
| Входной диаметр туннеля DВХ [см] | 7 | 6 | 5 | 4 | 3 | 3,4 |
| Выходной диаметр туннеля DВЫХ [см] | 7 | 7 | 7 | 7 | 7 | 7 |
| Длина туннеля L [см] | 15 | 15 | 15 | 15 | 15 | 15 |
| Общая проводимость туннеля Kо [см] | 1,877 | 1,673 | 1,452 | 1,212 | 0,950 | 1,057 |
| Резонанс ФИ в ящике fb [Гц] | 44,0 | 41,5 | 38,7 | 35,4 | 31,3 | 33,0 |
Первый вариант (*) – это цилиндрический туннель; расчёты конического туннеля (2…5 варианты) с DВХ=6…3 см показали, что нужный результат получается при входном диаметре в диапазоне 3см<DВХ<4см; и после уточнения имеем DВХ=3,4 см (6-й вариант).
4. В заключение по формуле Р. Смола (9) проверим минимально допустимый диаметр туннеля:
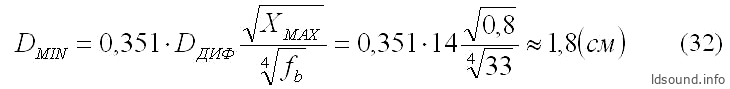
где:
- DДИФ [см] – диаметр диффузора динамика;
- XMAX [см] – максимальное осевое смещение диффузора динамика;
- fb [Гц] – резонанс ФИ.
Полученный наименьший диаметр туннеля DВХ=3,4 см почти в два раза превышает минимально допустимую величину DМИН≈1,8 см (″по Матараццо″ можно ещё меньше).
ИТОГИ РЕШЕНИЯ Для ящика объёмом V=30 л заданную частоту резонанса фазоинвертора fb=33 Гц можно получить, применяя конический туннель длиной L=15 см и диаметрами DВХ=3,4 см и DВЫХ=7 см. ЗАДАЧА РЕШЕНА.
Аналогичную частоту резонанса с цилиндрическим туннелем (с таким же выходным диаметром DВЫХ=7 см) возможно получить только при длине туннеля L≈30 см.
6.4. РАСЧЁТ ТУННЕЛЕЙ С ПЕРЕМЕННЫМ ПРЯМОУГОЛЬНЫМ СЕЧЕНИЕМ
При расчёте резонансной частоты fb прямоугольного туннеля с постоянным сечением ″по Эфрусси″ вводится коэффициент-поправка k, учитывающий соотношение сторон сечения, см. формулу (10).
Очевидно, что для расчётов прямоугольных туннелей с переменным сечением также следует применять указанную поправку; однако в большинстве случаев у таких туннелей эта поправка может быть также переменная по длине туннеля, и как в таком случае её применять(?..)
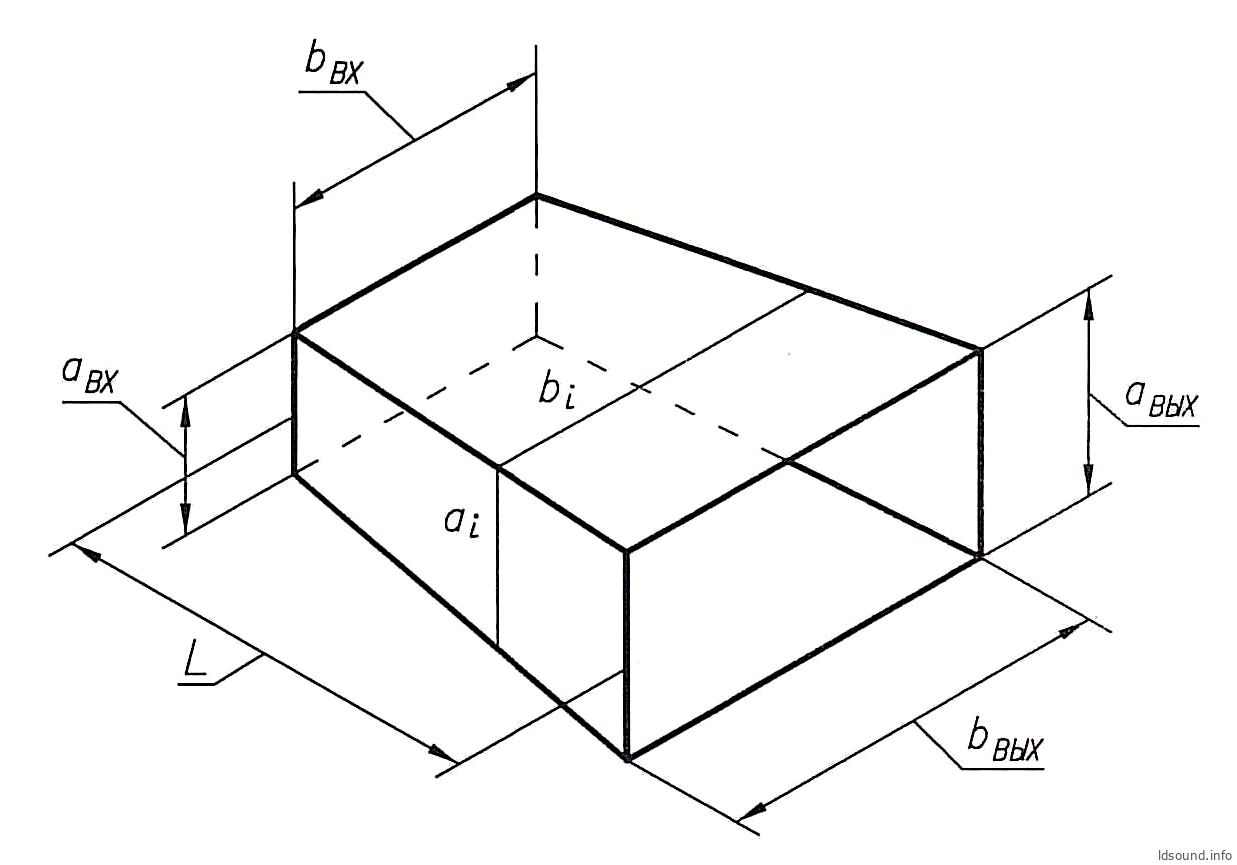
Рассмотрим сначала туннель с переменным сечением в виде усечённой пирамиды с прямоугольником в основании, см. рис. 8. Особенность данной конструкции в том, что если боковые грани туннеля продлить, то все они сходятся в одной точке – вершине пирамиды. Это означает, что соотношения сторон сечения будут равными для каждого сечения (из-за подобия треугольников при геометрических построениях), т.е.:
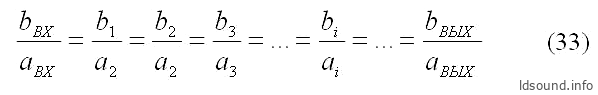
В итоге поправка k получается постоянная по всей длине туннеля, и расчёт осуществляется почти так же, как и для конического туннеля (с небольшими отличиями).
Нужно по аналогии поделить весь туннель по длине на N одинаковых сегментов, чтобы длины каждого сегмента L1=L2=L3=…=Li=…=LN – были бы одинаковые согласно формуле (25).
Следующим этапом нужно для каждого сегмента определить средние величины сторон прямоугольного сечения; т.е. для каждого сечения определить соответствующие пары размеров:
(a1, b1), (a2, b2), (a3, b3) … (ai, bi) … (aN, bN) (34)
Затем вычисляем проводимости для каждого сегмента:
Рис. 8. К расчёту туннеля в виде усечённой прямоугольной пирамиды:
И, наконец, вычисляем общую проводимость прямоугольного туннеля в виде усечённой пирамиды:
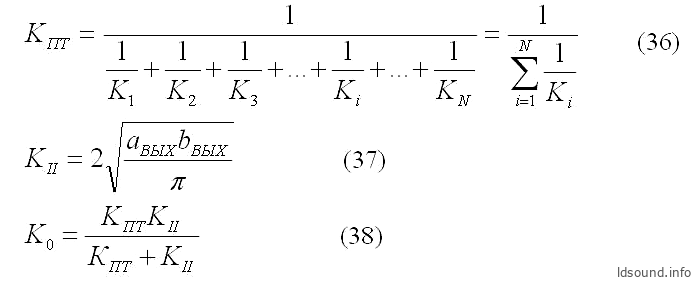
где:
- КПТ [см] – проводимость прямоугольного туннеля в виде усечённой пирамиды;
- КII [см] – проводимость отверстия в тонкой стенке с прямоугольным сечением, считается как эквивалентный диаметр по формуле (11);
- К0 [см] – общая проводимость прямоугольного туннеля;
- aВЫХ, bВЫХ [см] – стороны выходного сечения туннеля.
Резонанс такого туннеля считается по формуле (13), но с учётом поправки k:

где: k=(bi/ai) – поправка ″по Эфрусси″, причём k=const по всей длине туннеля (b>a).
В заключение рассмотрим прямоугольный туннель с переменным сечением, в котором соотношение сторон в сечении переменное по длине туннеля.
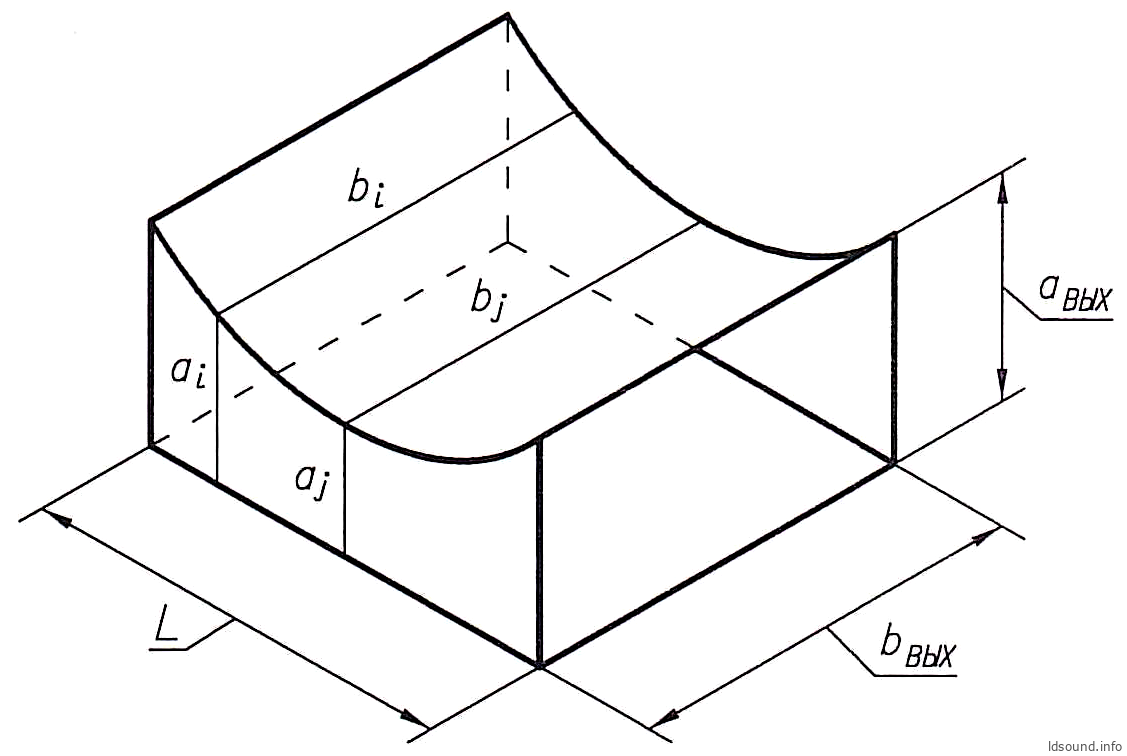
Покажем, как такой туннель может выглядеть на примере экспоненциального туннеля, см. рис. 9. Из представленной схемы очевидно, что в общем случае:

В таком случае целесообразно транспонировать формулу (39), а именно ″перенести″ поправку ki под корень (естественно, степень при поправке увеличится), более того – нужно включить эту поправку в проводимость, т.е.:
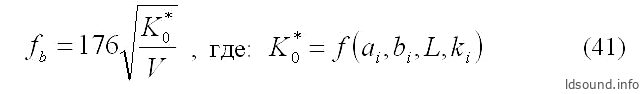
Теперь остаётся для каждого сегмента туннеля вычислять не только проводимости, но и поправку на соотношение сторон сечения; на самом деле, это несложно…
Рис. 9. Экспоненциальный туннель:
Первоначальные вычисления такие же, как и для туннеля в виде усечённой пирамиды. Т.е. нужно по аналогии поделить весь туннель по длине на N одинаковых сегментов, чтобы длины каждого сегмента L1=L2=L3=…=Li=…=LN – были бы одинаковые согласно формуле (25).
Следующим этапом нужно для каждого сегмента определить средние величины сторон прямоугольного сечения; т.е. для каждого сечения определить соответствующие пары размеров (ai, bi) [см], и рассчитать проводимости Ki каждого сегмента, как уже предлагалось выше по формулам (34) и (35).
А дальше начинаются отличия… Следует определить коэффициент-поправку для каждого сегмента туннеля (при условии, что bi>ai):
Окончательно вычисляем общую проводимость прямоугольного туннеля:
где:
- К*ПТ [см] – проводимость прямоугольного туннеля (в общем виде);
- КII [см] – проводимость отверстия в тонкой стенке с прямоугольным сечением;
- К*0 [см] – общая проводимость прямоугольного туннеля;
- kВЫХ – поправка для выходного сечения.
Здесь резонанс туннеля fb вычисляется по формуле (41), т.к. коэффициент-поправка предварительно уже был включён в проводимости каждого сечения.
7. ЛИТЕРАТУРА
- М.М. Эфрусси «Громкоговорители и их применение», изд. ″Энергия″, г. Москва, 1976 г., с. 70-78.
- Э.Л. Виноградова «Конструирование громкоговорителей со сглаженными частотными характеристиками», изд. ″Энергия″, г. Москва, 1978 г., с. 45-47.
- Ж.П. Матараццо «Фазоинвертор: короче!» (перевод с итальянского), ж. ″Автозвук″, 2001 г., № 10, с. 56.
- В.К. Иофе, М.В. Лизунков «Бытовые акустические системы», изд. ″Радио и связь″, 1984 г., с. 50-59.
- И.Б. Крендалл «Акустика» (перевод с английского), изд. ″ВЭТА″, г. Ленинград, 1934 г., с. 42-46.
P.S.
Особенные впечатления вызвало знакомство с книгой Крендалла; оказывается, ещё 100 лет назад уже было известно, как рассчитывать резонаторы Гельмгольца в общем виде. В приложении далее представлена копия титульной страницы книги.
2023 г.



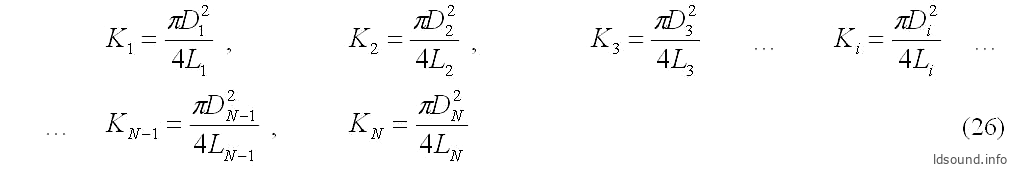
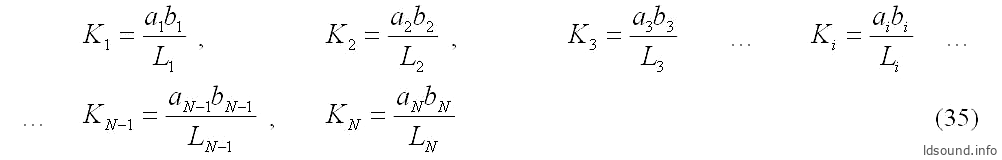
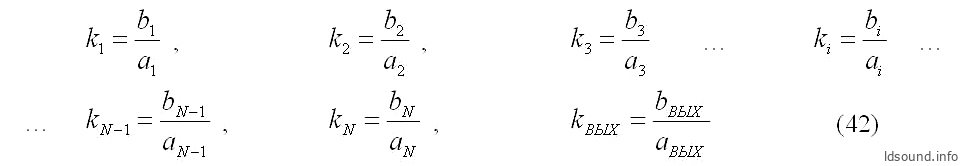

Всегда хотелось понять, как рассчитывать фазоинвертор, а более конкретно – как рассчитать частоту резонанса туннеля ФИ по его геометрическим размерам.
Простые круглые трубы не в счёт, т.к. соответствующие расчётные формулы содержатся в справочниках; речь идёт о “более сложных конструкциях”: прямоугольных туннелей, туннелей с переменным сечением, или для случаев применения нескольких произвольных туннелей.
Оказалось, что для “сложных случаев” практически невозможно найти нужные формулы…
Должен сказать, что именно статья Матараццо «Фазоинвертор: короче!» послужила для меня толчком к поиску решения ФИ в общем виде (надеюсь, что не допустил ошибок…)
При переносе статьи на сайт изменился стиль написания некоторых формул, некоторые рисунки были заменены другими, и (пока ещё) отсутствуют некоторые рисунки;
и, кстати, (пока ещё) на 17.09.23. статья на сайте представлена не в полном объёме…
Однако, принципиального значения это не имеет;
большое спасибо Дмитрию (LDS) за размещение статьи на сайте.
Тем не менее, для желающих могу предложить статью в оригинале;
ну… или, если можно так сказать – “ версию для печати”:
https://disk.yandex.ru/i/1JjS9cLiE0vZtA