Апериодически демпфированные акустические системы (перевод Шорта)

Перевод статьи Д.Э. Шорта, с сокращениями.

Пропущенные места заменены тремя точками: … (Курсивом и в скобках пишу комментарии). Подчёркивания и выделения – мои.

Аннотация

Выведена и исследована теория апериодически демпфированной акустической системы (АС) во временнОй и частотной областях. Обсуждены преимущества апериодической конфигурации над оформлением типа закрытый ящик (ЗЯ).

Апериодически демпфированная АС описана параметрами, которые применяются для ЗЯ, с некоторыми дополнениями. Создана реальная система, имеющая все преимущества апериодической конфигурации, и её качество сравнено с системой типа ЗЯ того же размера.

(Комментарий 1. Исходная Q_tc системы в оформлении ЗЯ была столь высокой, что панель акустического сопротивления (ПАС) была просто необходимой.)

Прилагается полное выведение теории ЗЯ и ЗЯ с ПАС, а также методы измерений всех требуемых параметров.

Признательность (пропущено)

Содержание (пропущено)

Список рисунков (пропущено)

Часть 1. Введение

Погоня за Хай-Фаем началась сразу по окончанию второй мировой войны, когда относительное экономическое процветание вместе с ответвлениями военных технологий сделали домашнее стерео доступным среднему потребителю.

…

Система типа ЗЯ получила широкое применение благодаря удовлетворительному качеству по разумной цене. Также не столь сложно разработать и воплотить её аналог с ПАС, который, при правильном выборе динамика, обеспечит широкую полосу низких частот (НЧ) и хороший импульсный отклик.

…

Для корректного звуковоспроизведения, включающего правильную тембральную окраску, локализацию инструментов и размеры звукового образа, пара динамиков, работающих в стереосистеме, должна быть максимально похожей.

(Комментарий 2. Последнее упомянуто в свете того, что с помощью ПАС есть возможность подогнать параметры пары динамиков в районе резонансной частоты.)

Правда и то, что большое количество динамиков работают не в оптимальных для них оформлениях в связи с ограничениями по объёму или стоимости последних, а также в связи с разбросом параметров динамиков. Это приводит к плохим характеристикам в частотной и временнОй областях, и, в итоге, к плохому звучанию.

Вопрос о требуемых характеристиках АС является темой безконечных споров, однако субъективные тесты показывают, что ими являются: АЧХ, несоответствие которой делает звучание систем очень разным, и правильная переходная характеристика, делающая звук реалистичным.Последнее является причиной того, что продуманных систем с фазоинвертором (ФИ), звучащих музыкально и аккуратно, мало, поскольку, в большинстве случаев, их переходные характеристики даже близко не так хороши, как у корректно сконструированных ЗЯ. Также этим объясняется потребность в более качественном изготовлении динамиков, предназначенных для работы в паре.

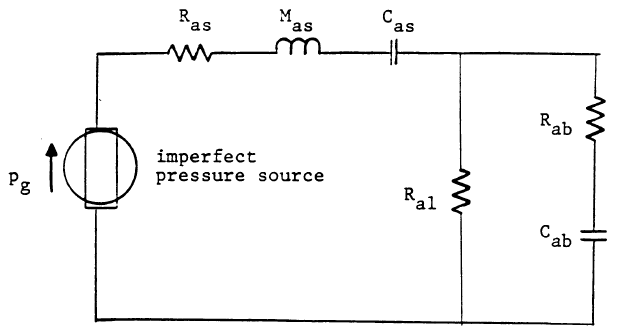
Предметом данной статьи является метод конструирования АС, подобных ЗЯ, но дополненных успокоителем перепада давления. Модификация имеет вид большого отверстия в ЗЯ, которое плотно заполнено пеной с открытыми ячейками, плотной тканью или волокнами дакрона.Отверстие позволяет системе немного «дышать», выравнивая большую разницу давлений между внутренним и внешним пространством ЗЯ. Демпфирование, производимое отверстием, практически не зависит от частоты в пределах интересующего нас диапазона, отсюда термин «апериодическое оформление».

Величина уменьшения перепада давления контролируется изменением количества и плотности заполнителя в отверстии и зависит от требований к системе. Гибкость данных параметров позволяет применять этот принцип в широких пределах условий с предсказуемым результатом.

Корректное внедрение ПАС позволит улучшить частотные и временнЫе характеристики большого количества АС, позволяя конструктору точно настроить ЗЯ согласно техническим требованиям или изначально получить преимущества от этого дополнения. Данный принцип применим в средне- и высокочастотных блоках, где также может быть полезен.

Система с ПАС сохраняет большинство преимуществ ЗЯ и, в большинстве случаев, приносит прекрасные результаты.

Часть 2. Определения

Используемые термины и определения будут те же, что и у Смолла, с некоторыми дополнениями.

Определения терминов

• Baffle – экран – структура, в которой вмонтирован динамик, обычно – передняя панель АС.
• Driver – драйвер, динамик – электромагнитный громкоговоритель как преобразователь, состоящий из магнитной системы (МС), звуковой катушки (ЗК), диффузородержателя, диффузора и т. д.
• Frequency Response – АЧХ – представляетсобой зависимость акустической мощности (при постоянной амплитуде подводимого к динамику напряжения) от частоты.
• Low Frequencies – низкие частоты, НЧ – все частоты, для которых 2πf< 2c/d, где d–диаметр драйвера, с = 344 м/с. Данное условие также выполняется, когда длина волны становится больше окружности драйвера.
• Speaker = драйвер.
• Speaker System– Акустическая Система, АС– законченная система, состоящая из драйвера (динамика), ящика, фильтра, материала заполнения и т.д.
• Variovent – вариовент, коммерческое изделие от Dynaudio, состоящее из пластмассовой корзины глубиной 25 мм и диаметром 125 мм, в которой находится заданное пользователем количество демпфирующего материала, помещаемое для внесения сопротивления потоку воздуха (дословно – flowresistance).

(Комментарий 3. Не знаю, был ли Вариовент единственным производимым вариантом ПАС в 1988 году, когда написана статья, но сильно смахивает на рекламу.)

Определения символов

В – индукция магнитного поля драйвера в воздушном зазоре

(Комментарий 4. Здесь и дальше в статье для упрощения принято В = const во всём зазоре.)

с – скорость звука в воздухе при Т=20°С, с = 344 м/с

C_ab– акустическая гибкость воздуха в оформлении (индекс а – acoustical, акустический; индекс b – box, ящик)

C_as – акустическая гибкость подвеса драйвера (s – self, собственный)

C_ms – механическая гибкость подвеса драйвера ( =C_as/S_d) (m – mechanical, механический; d – диффузор)

C_mes– электрическая ёмкость, соответствующая массе драйвера ( =M_asS²_d/(Bl)²) (там, где трииндекса подряд, е –equivalent, эквивалентный)

е_g– напряжение источника сигнала при разомкнутой цепи

f – частота в Герцах

f_s – резонансная частота динамика в свободном поле (freeair, фриэйр)

f_с – резонансная частота системы (драйвера в оформлении) (с –cabinet, в оформлении)

G(s) – комплексная передаточная функция

l – длина проводника ЗК в магнитном поле

(Комментарий 5. Здесь и дальше в статье принято Вl = constдля конкретного динамика.)

L_ces – электрическая индуктивность, соответствующая гибкости подвеса драйвера ( =C_as(Bl)²/S²_d)

L_vc – индуктивность ЗК (vc = voicecoil, ЗК)

(Комментарий 6. В статье индуктивностью ЗК при расчётах пренебрегают. То есть, формулы справедливы для достаточно низких частот, а статья ориентирована на ПАС для НЧ, в крайнем случае – мидбасового динамика.)

М_as – акустическая масса подвижной системы динамика, включающая массу присоединённого воздуха

М_ms – механическая масса подвижной системы динамика, включающая массу присоединённого воздуха ( =М_asS²_d)

Р_а – акустическая выходная мощность

Р_е – номинальная электрическая входная мощность (индекс е –электрический)

Q – добротность – отношение реактивного сопротивления к активному (последовательное соединение) или активного к реактивному (параллельное соединение)

Q_ec – Q драйвера на частоте f_с, учитывающая только электрические потери (R_е+R_g)

Q_es – Q драйвера на частоте f_s, учитывающая только сопротивление R_е

Q_mc – Q драйвера на частоте f_с, учитывающая только не электрические потери

Q_ms – Q драйвера на частоте f_s, учитывающая только не электрические потери

Q_ts – полная Q драйвера на частоте f_s, учитывающая все потери в системе (t–total, полный)

Q_tс – полная Q драйвера на частоте f_с, учитывающая все потери в системе

R_ab – акустическое сопротивление потерь в оформлении, возникающее из-за поглощения энергии внутри оформления

R_al – акустическое сопротивление потерь в оформлении из-за негерметичности (l – leakage, утечка)

R_as – акустическое сопротивление потерь в подвесе динамика

R_at – акустическое сопротивление всех потерь динамика

R_е – сопротивление постоянному току ЗК

R_es – электрическое сопротивление, соответствующее сопротивлению потерь в подвесе динамика ( =(Bl)²/(S²_dR_as))

R_g – выходное сопротивление источника или усилителя

R_ms – механическое сопротивление потерь в подвесе динамика

R_ar–акустическое сопротивление излучения (r – radiation, излучение)

s – комплексная частотная переменная (в данном случае s= jω =j2πf)

S_d – эффективная излучающая площадь диффузора динамика

Т – период (Т = 1/ω = 1/2πf)

u – линейная скорость

U–объёмная скорость

V_ab – объём воздуха, имеющий ту же акустическую гибкость, что и оформление ( = р₀с²С_ab)

(Комментарий 6. Заполнение оформления звукопоглощающим материалом (ЗПМ) приводит к увеличению гибкости оформления: она становится больше, чем у воздуха в том же физическом объёме.)

V_as – объём воздуха, имеющий ту же акустическую гибкость, что и подвес динамика ( = р₀с²С_as )

Z_vc(s) – функция входного импеданса ЗК

n – эффективность, КПД

p₀ – плотность воздуха ( = 1,18 кг/м³ при нормальных условиях)

w – ω – частота в радианах ( =2πf)

w_c – частота резонанса системы

w_s – частота резонанса динамика

& – соотношение гибкостей, C_as/C_ab

@_lс – фактор потерь на частоте f_с

@_ls – фактор потерь на частоте f_s

Автор должен извиниться за использование некоторых нестандартных символов в статье. Символ “j” эквивалентен физическому символу “i”, корню квадратному из -1. Другой нестандартный символ, используемый в тексте, – “pi”, число π.

Часть 3. Основной анализ

Анализ системы динамик+ящик хорошо освещён, и потому здесь обсуждается кратко.

Электрическая система

Электрическая система динамика состоит из усилителя, соединительных проводов и ЗК. Все элементы вносят в схему электрическое сопротивление, а ЗК, кроме того, и индуктивность. Сопротивления усилителя и проводов для удобства объединяют, все элементы соединены последовательно:

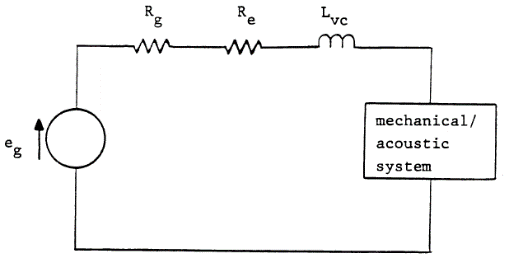
Поскольку мы рассматриваем работу динамика только в районе его резонансной частоты, то реактивное сопротивление ЗК значительно меньше остальных сопротивлений, и мы им пренебрегаем.

(Комментарий 7. ПАС, безусловно, оказывает воздействие на АЧХ и выше района резонансной частоты, слегка пропуская мидбасовые составляющие. Автор рассматривает только прямое излучение непосредственно от динамика и только в области механического резонанса.)

…

Часто более удобно представить усилитель как эквивалентный источник тока по Тевенину, с выходным током i_g = e_g/(R_g+R_e):

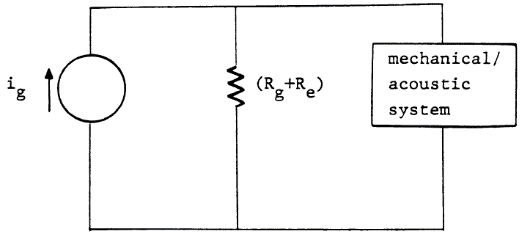
Механические и акустические системы

…

Подвесы вносят гибкость и механические потери в систему, подвижные элементы вносят массу. Внутренняя сторона излучающего конуса соединена с объёмом внутри ящика, вносящим свою гибкость и потери на поглощение энергии и негерметичность (щели). Сопротивление излучения также имеет место с обеих сторон конуса. Если давление в ящике равно р, то сила, приложенная к подвижной системе равна

F = pS_d                                 (1),

где S_d – эффективная площадь диффузора. Таким образом, диффузор работает как трансформатор механической системы в акустическую, с коэффициентом трансформации 1:S_d.

Механическая система может быть представлена в следующем виде:

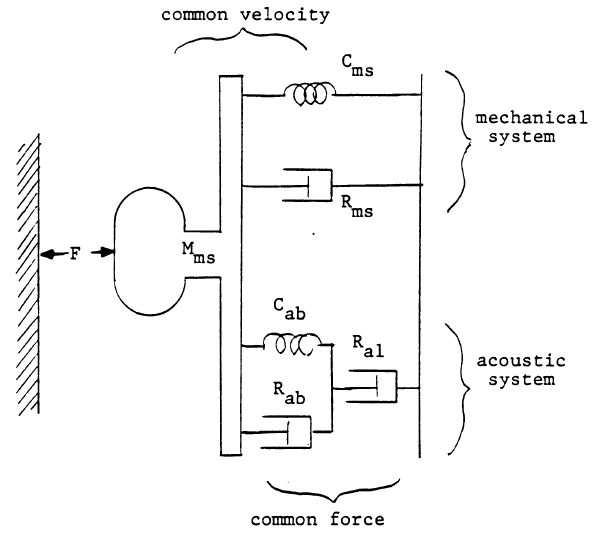
Система является вариантом колебательной системы с внешним возбуждением. Уравнение колебаний следующее:

F = Md²x/dt² + Rdx/dt + (1/C)x                                (2),

где F – сила, M – движущаяся масса, R–сопротивление движению (демпфирование), C–гибкость (величина, обратная коэффициенту жёсткости k), x – смещение.

Данное уравнение идентично уравнению колебаний в RLC контуре, если произвести следующие замены:

Сила = напряжение
Масса = индуктивность
Демпфирование = сопротивление
Гибкость = ёмкость
Смещение = заряд

Полный анализ системы возможен при применении теории электрических цепей. Элементы с одинаковой скоростью соединяются последовательно, а находящиеся под действием одинаковой силы – параллельно. Для акустической системы аналогия та же, только элементы, находящиеся под одинаковым давлением, включаются в параллель, а элементы с одинаковой объёмной скоростью – последовательно:

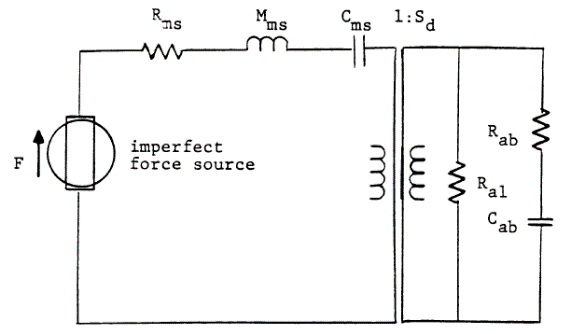
Поскольку диффузор работает трансформатором, то все механические элементы могут быть преобразованы в акустические, а источник силы – в источник давления:

Где:

Теперь можно анализировать систему как в механической, так и в акустической форме.

Связь между электрической и механической схемами

Электрическая и механическая (значит, и акустическая) системы взаимосвязаны через ЗК динамика. Для упрощения рассмотрения сопротивление ЗК постоянному току отделим от собственно ЗК. Сила, действующая на диффузор, и соответствующее ей акустическое давление при прохождении тока i через ЗК будут равны:

F = Bli (механическая модель)                               p = Bli/S_d (акустическая модель)           (4)

…

Также, когда диффузор движется с линейной скоростью u, или c акустической объёмной скоростью U, в звуковой катушке генерируется противоЭДСE_mf:

E_mf=Blu                                                E_mf = BlU/S_d                                                       (5)

Или

Таким образом, элементы импеданса на одной стороне схемы проявляют себя с другой, но их связь – обратно пропорциональная.

(Комментарий 8. По этой причине увеличение механических потерь в подвижной системе динамика, как и установка ПАС, приводит к уменьшениюэлектрического импеданса в районе частоты механического резонанса. Что необходимо учитывать в схеме замещения динамика при: пропитке подвеса полиизобутиленом, установке в ЗЯ/ЗЯ с ПАС, заполнении объёма ЗПМ.)

Элементы эквивалентной схемы

А) Сопротивление.

Механический и акустический эквиваленты электрического сопротивления:

Электрический эквивалент механического R_m или акустического R_a сопротивления:

Б) Масса.

Электрический эквивалент механической и акустической массы:

Обратите внимание, что механическая и акустическая массы, являющиеся по своей природе аналогом индуктивности, в электрической схеме становятся ёмкостями.

В) Гибкость.

Электрический эквивалент механической гибкости C_m и акустической гибкости C_a:

Заметьте, что механическая и акустическая гибкости, являющиеся по своей природе аналогом ёмкости, в электрической схеме становятся индуктивностями.

(Комментарий 9. Отсюда следует правильность коррекции электрической схемы замещения динамика при установке его в ЗЯ уменьшением индуктивности: https://ldsound.club/index.php?threads/sxemy-zameschenija-dinamikov.475/post-16549)

Г) Электрическая ёмкость.

Механическим и акустическим эквивалентом электрической ёмкости выступает масса:

Д) Индуктивность.

Механическим и акустическим эквивалентом индуктивности будет гибкость:

Е) Механические системы, движимые с одинаковой скоростью.

Механические элементы, движимые с одинаковой скоростью, будут аналогом элементов с одинаковым протекающим током. Таким образом, их механические сопротивления суммируются как последовательно соединённые элементы:

что является параллельным электрическим соединением элементов. То есть, последовательно соединённые элементы механической схемы проявятся как параллельно соединённые элементы в электрической схеме. То же самое справедливо для акустических элементов, с подстановкой BL/S_dвместо BL и объёмной скорости вместо линейной.

Ж) Механические элементы с одинаковой приложенной силой.

Элементы с одинаковой приложенной силой в механической схеме являются соединёнными параллельно, и их общее механическое сопротивление:

Таким образом, элементы с одинаковой приложенной силой в механической схеме проявляют себя как последовательно соединённые элементы в электрической. То же самое справедливо для акустических элементов, с соответствующей подстановкой BL, силы и скорости.

З) Последовательное и параллельное соединение электрических элементов.

Применив те же соображения, что и в двух предыдущих пунктах, приходим к выводу, что параллельные подключенные электрические элементы будут представлены как последовательно соединённые механические, а последовательно подключенные электрические – как параллельно соединённые механические.

И) Механические эквиваленты электрического напряжения и тока.

Таким образом, электрическое напряжение становится механической или акустической скоростью, а источник напряжения – источником линейной или объёмной скорости.

Принимая во внимание (4), получим, что электрический ток становится механической силой или акустическим давлением, а источник тока – источником силы или давления.

…

Полные эквивалентные схемы

С учётом приведённого выше, полная эквивалентная акустическая схема имеет вид:

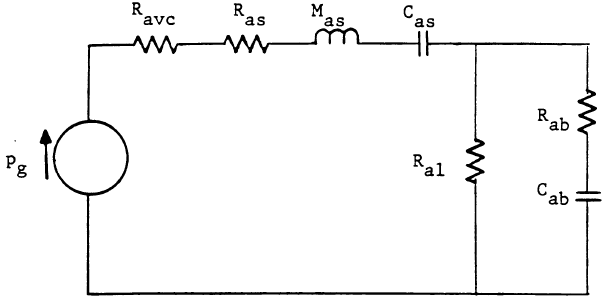
Где

Сопротивление излучения R_ar, появляющееся в любой излучающей части, игнорируется, поскольку оно обычно меньше, чем 1% от потерь в системе, хотя и отвечает за весь акустический выход.

Полная эквивалентная электрическая схема имеет вид:

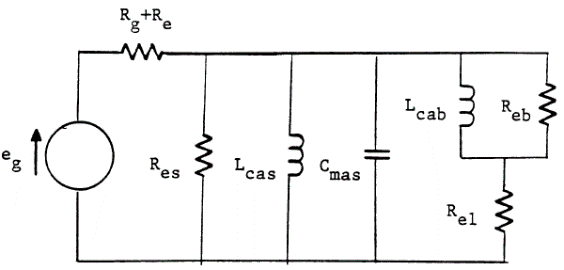
Где:

• e_g – выходное напряжение усилителя,
• R_g – выходное сопротивление усилителя,
• R_e–сопротивление ЗК,
• C_mas–эквивалентная масса подвижной системы,
• L_cas–эквивалентная гибкость подвеса динамика,
• R_es – эквивалентные потери в подвесе динамика,
• L_cab–эквивалентная гибкость оформления,
• R_eb–эквивалентные потери в оформлении (заполнении),
• R_el–эквивалентные потери на негерметичность.

Общая передаточная функция

Акустическая схема может быть представлена в общем виде так:

:

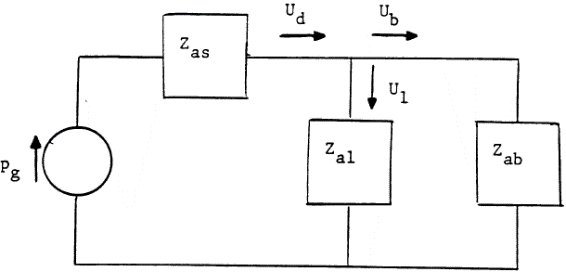
Здесь:

• Z_as – импеданс драйвера,
• Z_ab – импеданс оформления,
• Z_al – импеданс цепи, отвечающей за утечки,
• U_d – объёмная скорость в ветви динамика,
• U_b – объёмная скорость в оформлении,
• U_l – объёмная скорость через щели.

Выражение для эффективности системы (КПД):

n = P_a/P_e                                                                            (24)

Здесь:

P_e = i²R_e = e_g²R_e/(R_g+R_e)²                                                            (25)

В то же время, акустическая мощность:

P_a = |-U_d + U_l|²R_{a r}                                                                                      (26)

a                           U_d = U_b + U_l                                                                       (27)

и, как следствие,

|-U_d + U_l|² = |U_b|²                                                                                     (28)

Тогда КПД можно записать как:

n = R_ar|U_b|²(R_g + R_e)²/(e_g²R_e)                                    (29)

(Комментарий 10. Обратите внимание, что U_l, объёмная скорость в щелях, она же – в ПАС, котораяесть негерметичность с регулируемым параметром, может только уменьшать полезную составляющую U_b (следует из (27)). Отсюда неутешительный вывод: ПАС ни при какой настройке не может быть эффективнее исходного ЗЯ, кроме случая паразитного резонанса по принципу фазоинвертора, см. приложение Б.)

Далее, анализ последнего рисунка приводит к следующему:

U_d = p_g/ (Z_as + Z_ab + Z_asZ_ab/ Z_al)                                   (30)

На НЧ сопротивление излучения не зависит от размера излучателя и равно:

R_ar = p₀w²/2πc                                                                 (31)

Объединяя (29), (30) и (31), получаем:

n = (BL / S_d)² (p₀ / (2πcR_eM_as²)) (|sM_as/ (Z_as + Z_ab + Z_asZ_ab/ Z_al) |)²        (32)

Или:

n = (BL / S_d)² (p₀ / (2πcR_eM_as²)) |G(s)|²,                          (33)

где G(s) – комплексная передаточная функция динамика, вобравшая в себя ВСЕ зависящие от частоты переменные, в то время как два первых сомножителя частотнонезависимы.

Значение передаточной функции

Обобщённая передаточная функция G(s) справедлива для всех драйверов прямого излучения. Это есть выражение для акустического выхода при постоянной амплитуде подводимого напряжения, в области НЧ. С точностью до постоянной, модуль G(s) есть АЧХ АС.

Часть 4. АС типа ЗЯ

Закрытые системы легко анализируются на основе их эквивалентной электрической схемы.

Анализ системы типа ЗЯ. Акустическая схема

Практически, ЗЯ не должен иметь значительную негерметичность, и R_al можно игнорировать. Потери в ящике, вызванные наличием распорок и заполнением внутреннего объёма звукопоглощающим материалом (ЗПМ) (обычно используется дакрон или длинноволокнистая шерсть) просто малы по сравнению с потерями в подвесе на НЧ, и также игнорируются.

(Комментарий 11. В нормальном ЗЯ R_al и влияние распорок, конечно, надо игнорировать. Но с R_ab ситуация иная. Заполнение объёма большим количеством ЗПМ существенно изменяет параметры системы. Во-первых, это увеличивает гибкость оформления L_cab, что приводит к одновременному уменьшению Q_tc и f_c. Дополнительно, добротность уменьшится влиянием R_ab (см. статью «Закрытый ящик: полвека истории и большое будущее»). Следовательно, снижение Q_tc заполнением объёма ЗЯ ЗПМ-ом имеет преимущество по сравнению с применением ПАС, поскольку второй НЕ снижает резонансную частоту. Автору упоминать об этом некогда, он занят ПАС.)

Если в эквивалентной акустической схеме ЗЯ удалить сопротивление утечек R_al, закоротить сопротивление потерь R_ab, а C_as и C_ab объединить в C_at, то получим упрощённую схему, подобную последовательному RLC контуру:

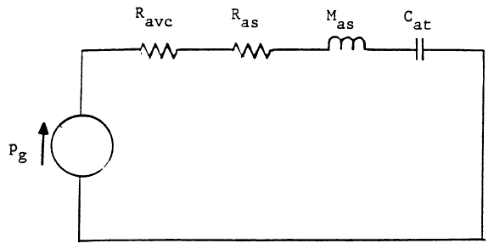
Для электрической схемы, частота резонанса и добротности будут определяться как:

(полная добротность)

Заметьте, что если ящик отсутствует, то достаточно положить C_at = C_as.

Для динамика в свободном поле (freeair) имеем:

Параметры динамика в свободном поле являются фундаментальными и полностью определяют все возможные настройки АС типа ЗЯ с заданным динамиком.

(Комментарий 12. Логичнее было бы сначала описать динамик в свободном поле уравнениями (38)-(41), а потом засунуть его в ЗЯ с уравнениями (34)-(37), но что уж есть.)

Значение термина «добротность»

Добротность есть «избирательность» резонанса. Она рассчитывается по импедансу (механическому, электрическому или акустическому) системы и описывает демпфирование. Как мы увидим позже, добротность связана с амплитудой передаточной характеристики вблизи резонанса.

Если записать уравнение гармонических колебаний системы с потерями как:

(Комментарий 13. Заметьте, что частота свободных затухающих колебаний системы w_d не совпадает с частотой резонанса при вынужденных колебаниях w₀. Например, при полной добротности динамика в ЗЯ Q_tc = 0,707 (второй порядок по Баттерворту) w_d = 0,707w₀, что дополнительно уменьшает заметность переходного процесса, поскольку ЗЯ излучает частоты ниже резонанса с большим ослаблением.)

При большом значении Q система плохо демпфирована – переходная характеристика имеет колебания на протяжении нескольких периодов w_d.

Передаточная характеристика АС типа ЗЯ

В общем случае передаточная функция имеет вид (32).

Для упрощённой схемы ЗЯ функция сокращается до:

Нормализуя подстановкой s_n = sT_c, получаем:

передаточную функцию нормализованного ФВЧ второго порядка в стандартной форме, с формальной константой 1/Q_tc.

(Комментарий 14. Для развеселения читателя автор в последнем блоке формул применяет скобки трёх видов, молодец…)

Максимально упрощённая эквивалентная акустическая схема ЗЯ:

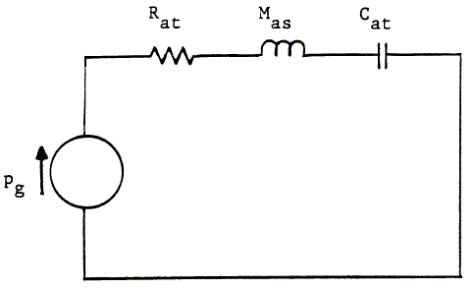
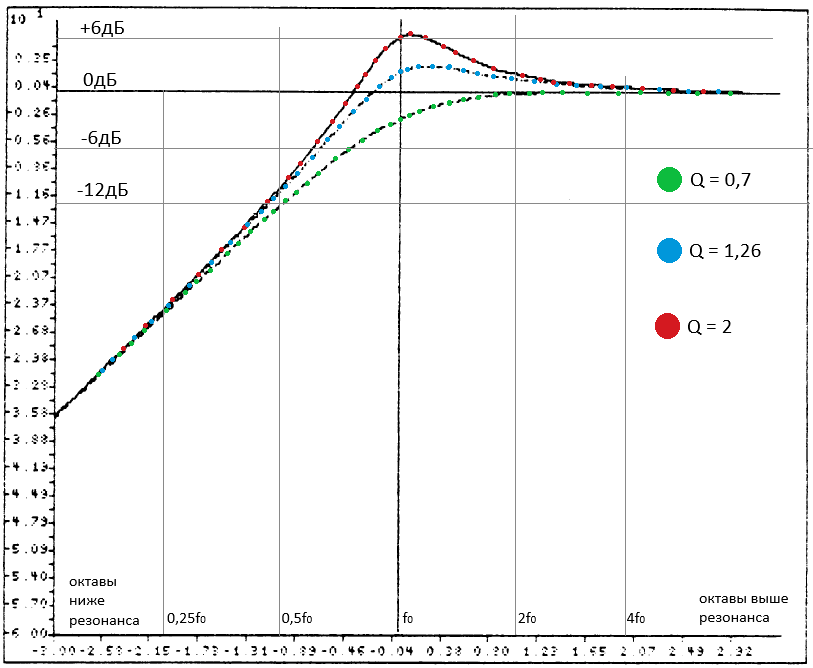
Графики модуля G(s) для разных Q_tc приведены ниже.

(Комментарий 15. Ввиду ужасного качества сканированных рисунков мне пришлось дорисовать координатные сетки и обозначить кривые цветом.)

…

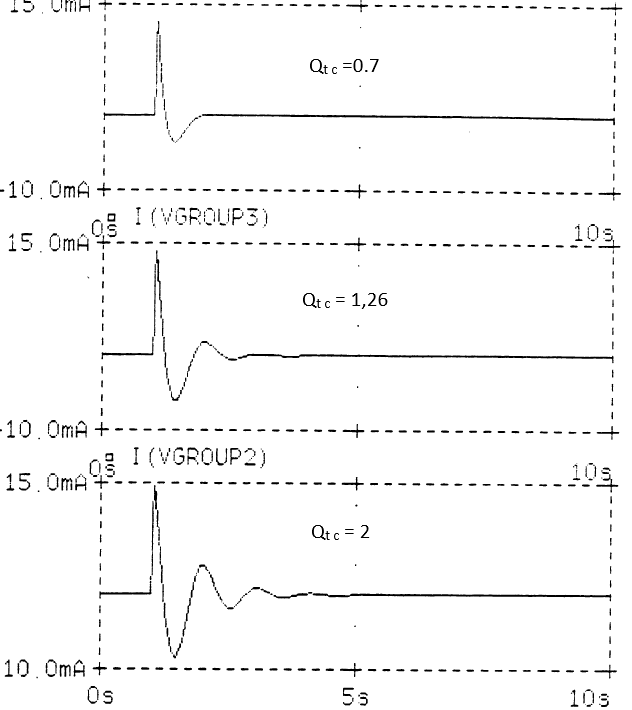
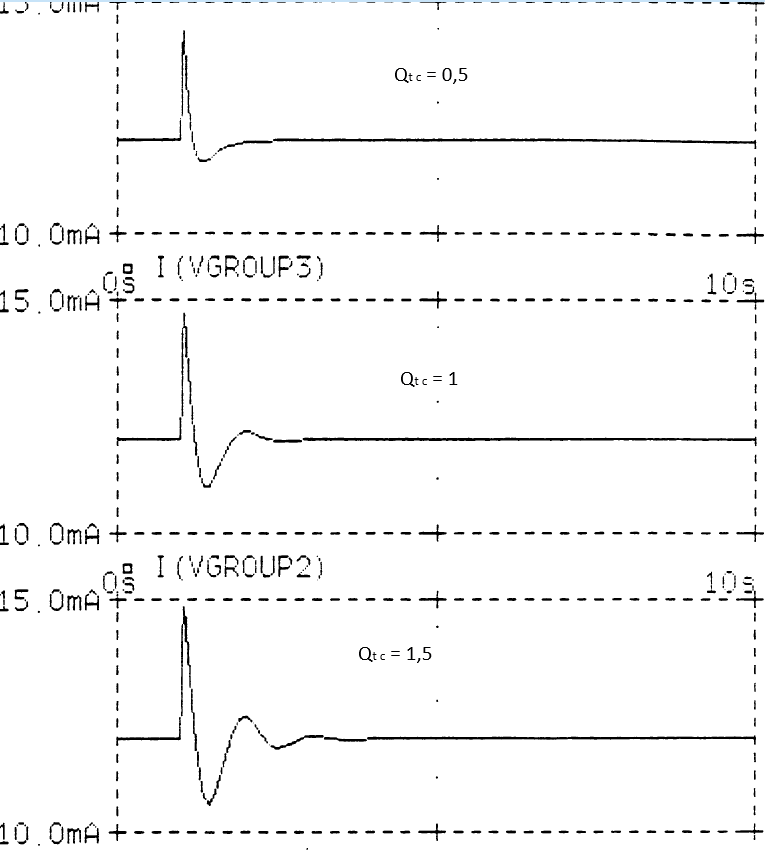
Импульсные характеристики для некоторых значений Q_tc приведены ниже. Заметьте, что увеличение Q_tc приводит к росту амплитуды в районе резонанса, одновременно переходная характеристика (ПХ) показывает продолжительное затухание колебаний.

 

Конструирование АС типа ЗЯ (пропущено)

Обсуждение АС типа ЗЯ

Качество АС типа ЗЯ легко определить по её передаточной характеристике. Пик отдачи возле резонанса зависит от Q_tc, а крутизна ската чуть ниже резонансной частоты равна 12 дб/октаву. Изучение графиков для разных Q_tc показывает, что при Q_tc>1 крутизна ската сразу ниже резонанса чуть больше 12 дБ/октаву, достигая 18 дБ/октаву при бОльших значениях Q_tc, в то время как при Q_tc<0,8 крутизна ската в этой области около 6 дБ/октаву. ПХ при Q_tc>1 характеризуется существеннымиколебаниями на протяжении нескольких периодов. Слышимый эффект продолжительного затухания называют «панчовым» басом, вместе с пиком на АЧХ при больших Q_tc он приводит к более выраженному, глубокому басу. Такой тип звучания предпочтителен для большинства направлений современной электронной музыки, «настоящее» звучание которой никто не слышал. Однако классическая музыка, записанная без электронной обработки, на системах с высокой Q_tc звучит очень ненатурально. Поскольку классическая музыка может быть сравнена с оригиналом, то приходим к выводу, что реалистическое воспроизведение живой музыки есть мера качестваАС.

Анализ уравнения ((64), см. оригинал) показывает, что для получения низкого значения Q_tc требуется либо драйвер с низкой Q_ts, либо большой ЗЯ, либо часто выполнение обоих условий. Низкая Q_ts требует значительного электромагнитного демпфирования, благодаря большой магнитной системе, что приводит к удорожанию. Большой объём ЗЯ потребует применения конструкций с большой площадью стенок, вибрации которых существенно окрашивают звучание. Адекватное демпфирование резонансов стенок потребует их утолщения, что увеличивает расходы. Устранение резонансов стенок потребует также установки внутренних распорок, что ведёт к дальнейшему удорожанию. Наиболее дешёвый путь – минимизация излучения стенок изготовлением корпуса минимальных размеров – приводит к повышению Q_tc.

Однако наиболее притягательным свойством АС типа ЗЯ является простота их изготовления. Рассмотрение системы ЗЯ чётко показывает, что динамик с любой заданной Q_ts будет работать в широком диапазоне настроек, задаваемых только объёмом ящика. Поскольку сделать ЗЯ одинакового объёма очень легко, то повторяемость результатов отличная. Правда, это справедливо для драйверов с одинаковыми параметрами.Изменения Q_ts и C_as более чем на 75% (?) коренным образом изменяют качество системы, приводя к несоответствию пары АС. Единственный путь откорректировать это – изменить объём ЗЯ, что трудоёмко и долго.

Как будет показано ниже, ПАС может облегчить решение данных проблем. Системы сдинамиком с высокой Q_ts и, следовательно, высокой Q_tc могут быть сделаны так, чтобы работать как системы с намного меньшей Q_tc, без ущерба для протяжённости диапазона в сторону НЧ. Системы, в которых динамик вынужден работать в малом объёме ЗЯ и, следовательно, с высокой Q_tc, могут быть улучшены до уровня систем с гораздо более низкой Q_tc, но небольшие потери баса из-за маленького ящика не исправимы. Наконец, совпадение АЧХ системы с требуемой вблизи резонанса легко выполняется изменением количества демпфирующего материала в отверстии ПАС, что потребует немного времени и работы.

(Комментарий 16. Как видим, статья посвящена разработке не МАКСИМАЛЬНО КАЧЕСТВЕННОЙ, а МАКСИМАЛЬНО ДЕШЁВОЙ в изготовлении и наладке конструкции АС, в случаях ограничения по объёму и/или наличия высокодобротного динамика.)

Часть 5. АС с ПАС

АС с ПАС подобны АС типа ЗЯ, но они улучшены благодаря ПАС (pressurerelief) для увеличения демпфирования в системе. Основные параметры конструкции АС типа ЗЯ применяются для описания АС с ПАС, только с добавлением параметра, определяющего потери на негерметичность (leakageloss).

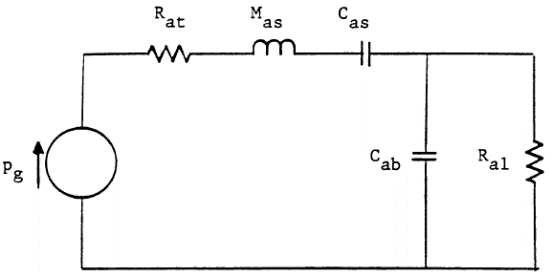
Акустическая схема ПАС

Акустическая эквивалентная схема системы с ПАС приведена ниже. На ней Вы опять не увидите R_ab. Все параметры динамика и ящика постоянны, кроме R_al. Систему принято называть апериодически демпфированной, поскольку R_al не зависит от частоты, и постоянная времени R_al×C_ab не является функцией драйвера или частоты резонанса системы.

Основываясь на (32), для АС с ПАС получаем:

Тогда:

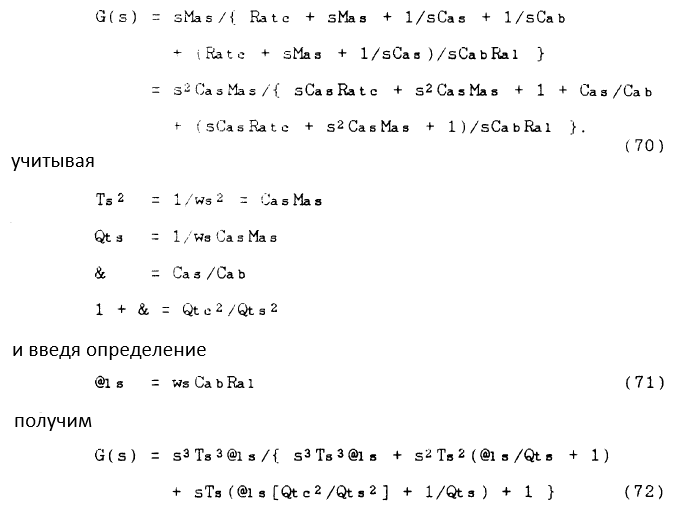
Что является выражением для ФВЧ третьего порядка нестандартной формы. Передаточную функцию как функцию резонансной частоты системы получим, используя:

Заметьте, что при @_lc>>1 (или при R_al>>1, при поддержании C_ab = const), выражение (77) сокращается до (55), описывающего передаточную функцию ЗЯ.

Анализ передаточной функции

Стандартная форма ФВЧ третьего порядка:

Единственным отличием (77) от (78) является наличие последней величины, Q_ts²/Q_tc². Из анализа ЗЯ мы знаем, что всегда выполняются неравенства Q_ts<Q_tc , (Q_ts²/Q_tc²) < 1.

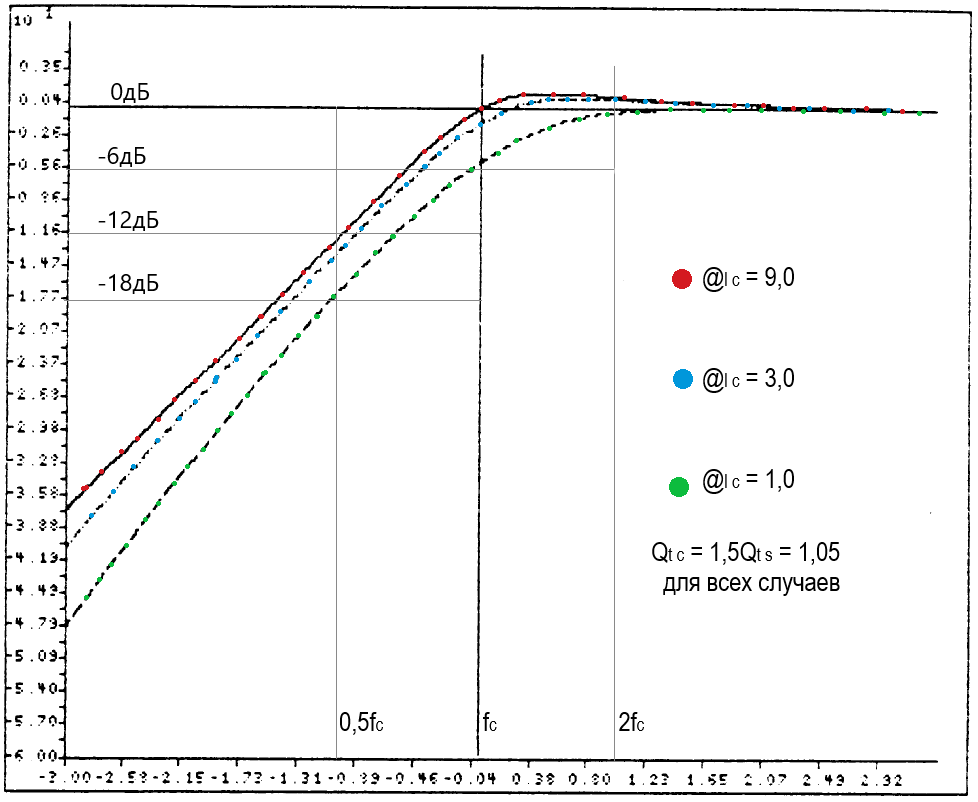
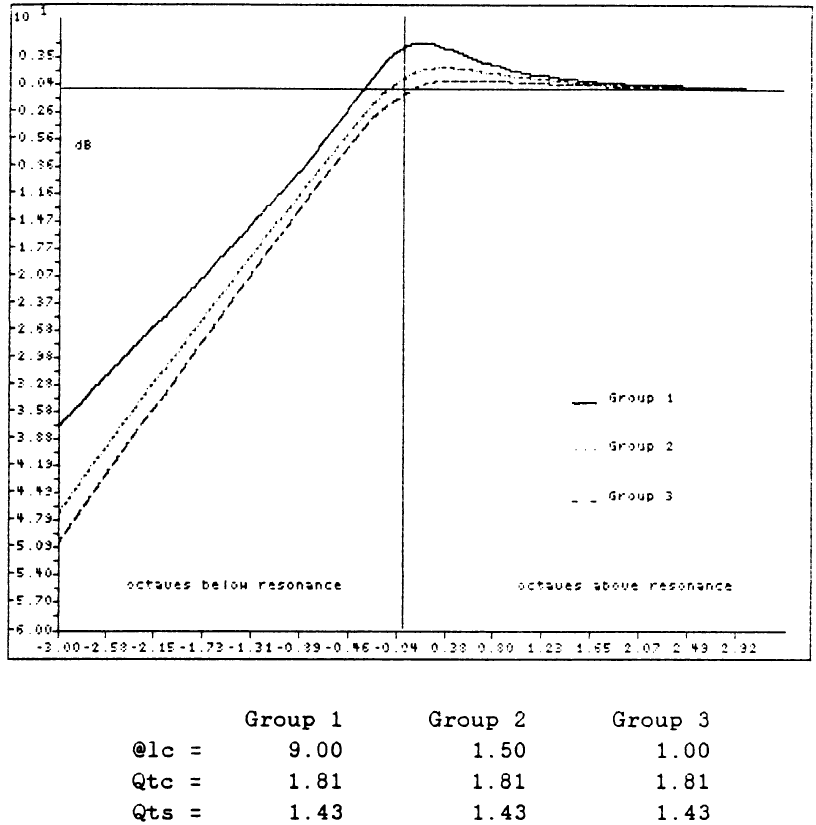
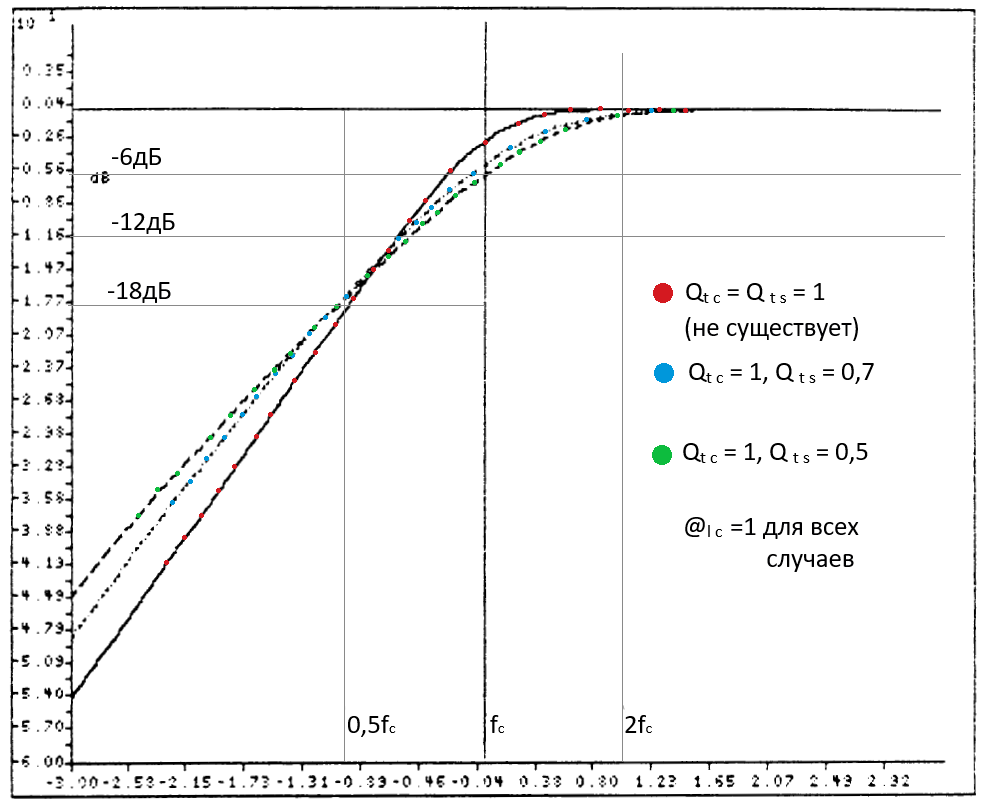
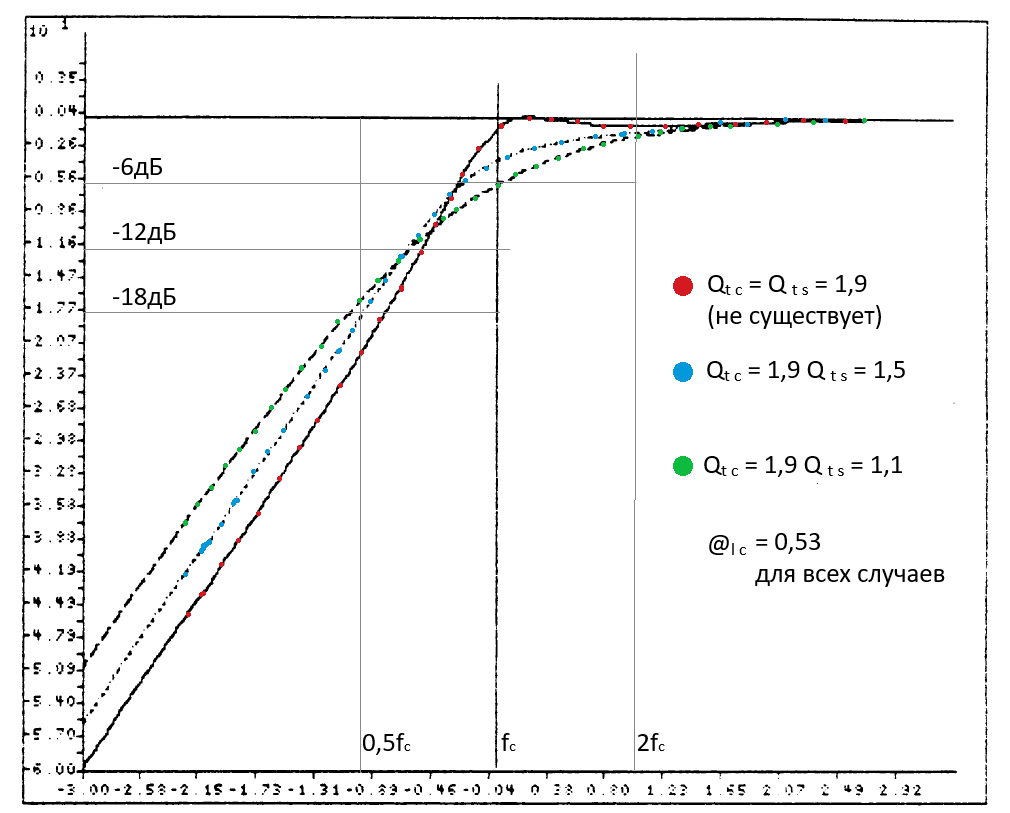
Графики передаточной функции G(s) для некоторых наборов значений @_lc, Q_tc, Q_ts приведены ниже. В каждом случае в качестве опорной для сравнения приведена стандартная функция Чебышёва третьего порядка (то есть, Q_tc = Q_ts = 1/@_lc). Заметьте, что во всех случаях стандартная форма имеет более плоскую АЧХ возле частоты резонанса системы, чем модифицированная форма, но скат у стандартной формы значительно круче.

(Комментарий 17. На приведенных выше рисунках варианты с Q_ts = Q_tc, красные точки, физически неосуществимы, графики – для общего образования. Два других графика следует читать так: взяли два динамика с разными Q_ts, поместили в ЗЯ, подобрали их объём так, чтобы Q_tc стала одинаковой, и применили ПАС с одинаковым значением величины @_lc. Что получилось – то и нарисовали. Обратите внимание, что влияние ПАС на ЗЯ снижается при: увеличении резонансной частоты динамика в свободном поле, увеличении объёмаC_ab, увеличении сопротивления ПАС R_al, то есть, при увеличении @_lc. Формула (71).)

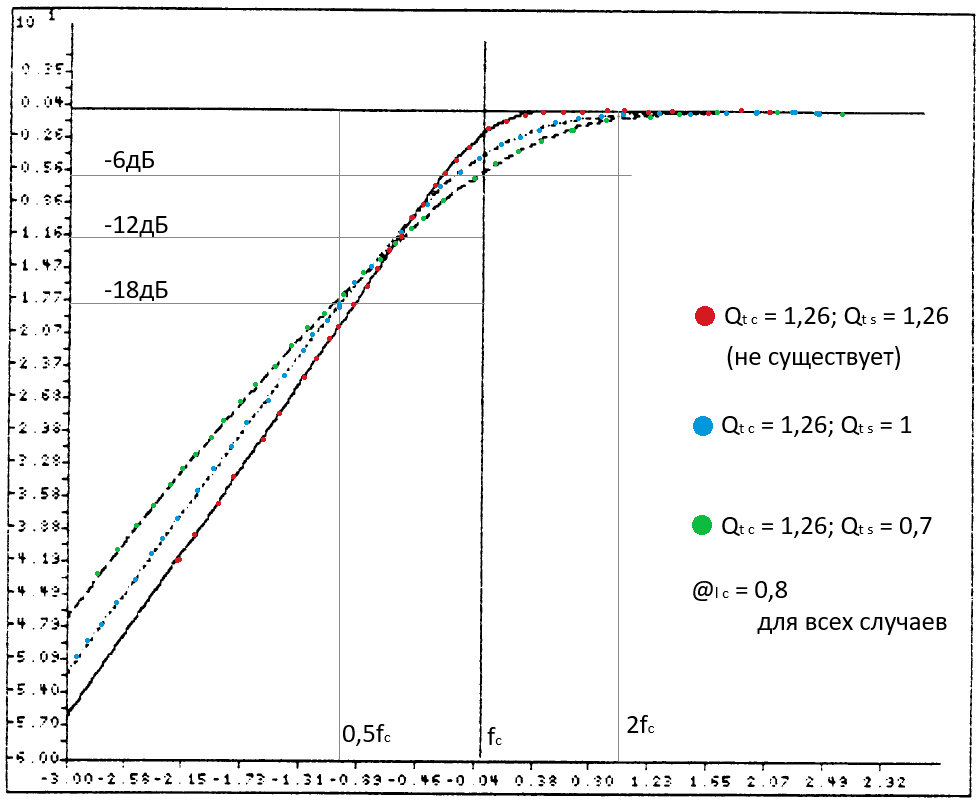
В ЗЯ высокая Q_tcприводит к увеличению КПД возле резонанса, крутому срезу непосредственно ниже резонанса и к плохой ПХ. В частотной области стандартная форма ФВЧ третьего порядка показывает похожие характеристики. Во временнОй области исследование стандартной формы в натуре невозможно, поскольку реализовать условие Q_ts=Q_tc физически не получится. Однако, система может быть просимулирована на компьютере. Это и было сделано с помощью симуляции схемы в PSpice-программе. Результаты для Q_tc = 1/@_lc = 1,26 приведены ниже.

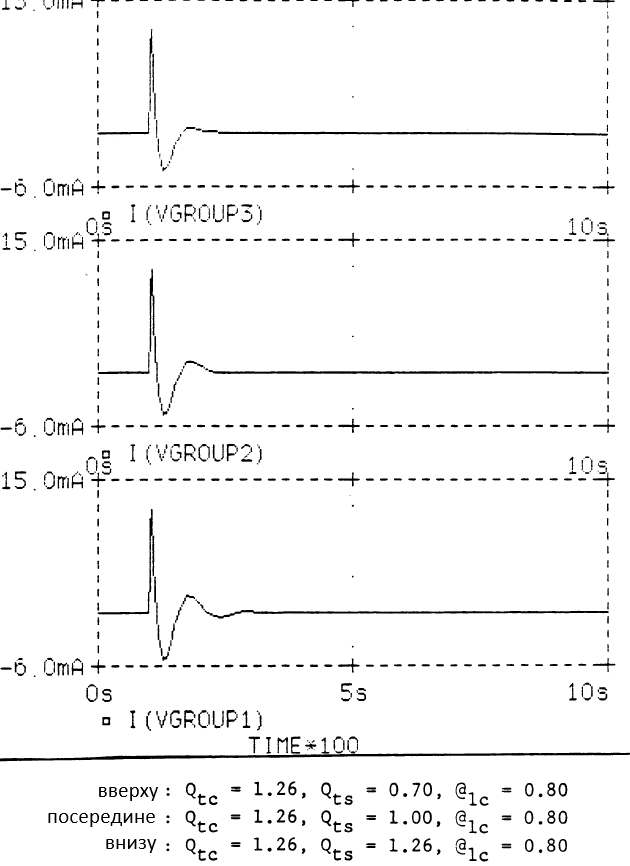
Заметьте, что колебания на графикеПХ уменьшаются по амплитуде и длительности для Q_ts<Q_tc. Сравнение системы ЗЯ с ПАС с системой ЗЯ при той же Q_tc показывает, что первая имеет значительно лучшую ПХ.

(Комментарий 18. Ничего удивительного, в ЗЯ с завышенной добротностью внесли активные потери. А динамик с более низкой исходной Q_ts оказался лучше…)

 

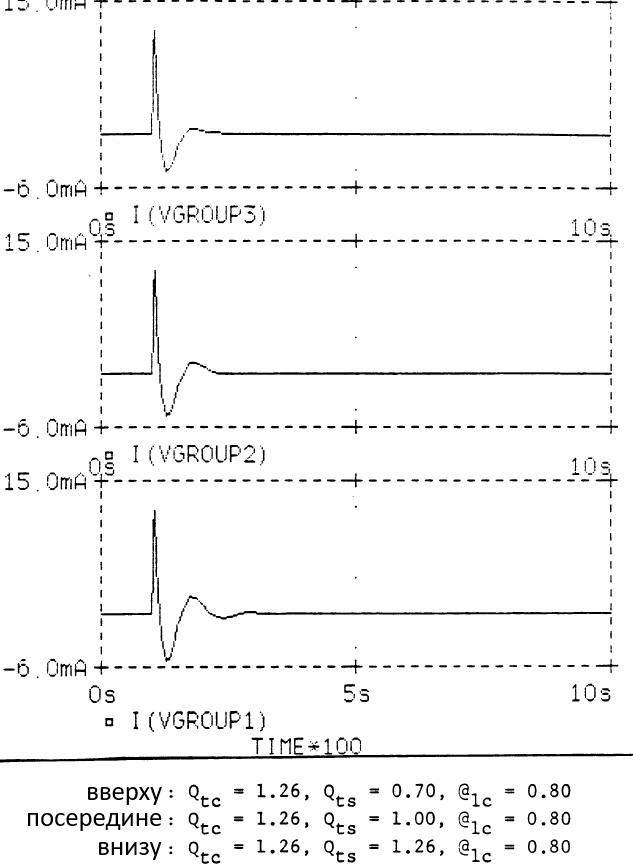
Сравнение стандартной и модифицированной форм показывает, что для последней ПХ улучшается при уменьшении исходной Q_ts, а крутизна ската ниже резонанса при этом немного уменьшается, ценой отхода АЧХ от максимально плоской.

Требуемые характеристики

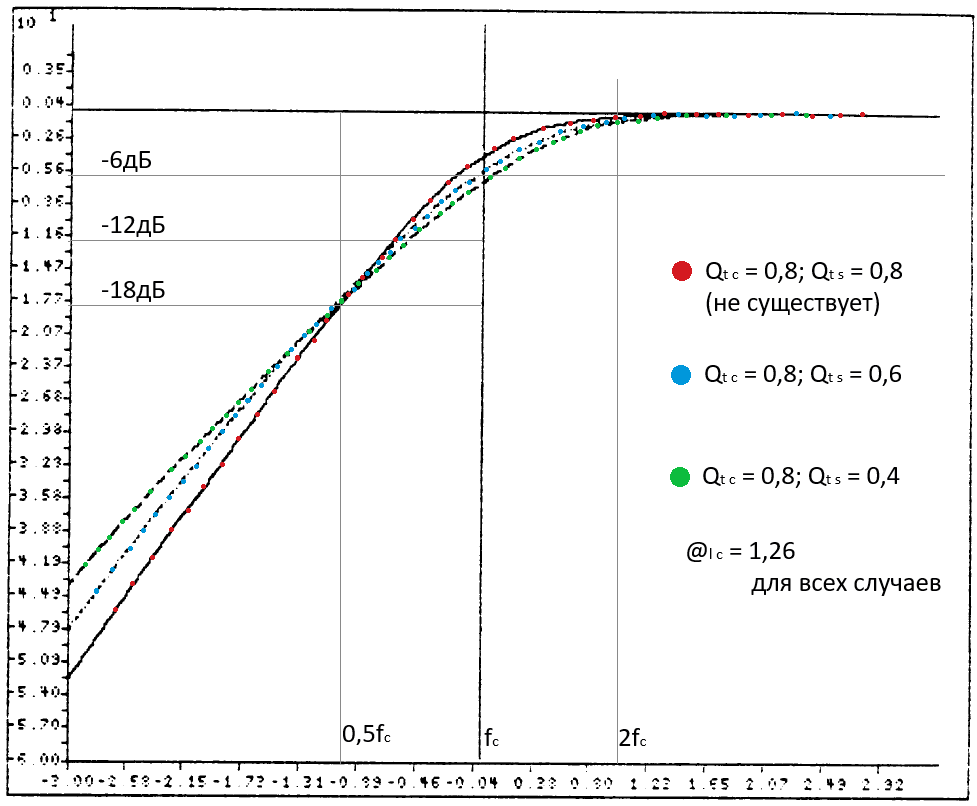
До этого момента вопрос о требуемых характеристиках не решён. Кое-кто думает, что плоская АЧХ в максимально широком диапазоне частот приведёт к наиболее точному воспроизведению, но субъективно это не так. Хотя гладкая АЧХ и необходима для точности, но хорошо контролируемая ПХ гораздо более важна для создания реалистичности звукового впечатления. Это тот случай, когда ухо более чувствительно к информации во временнОй области, чем в частотной. Для случая ЗЯ системы с Q_tс = 0,5…0,8 решительно более точны музыкально, чем ЗЯ с более высокой Q_tс.

(Комментарий 19. Обратите внимание на указанный диапазон Q_tс для хороших ЗЯ. К нему мы вернёмся в выводах.)

Исследование системы с ПАС

Нами были исследованы АЧХ и ПХ системы, описанные ФВЧ третьего порядка по Чебышёву для стандартной и модифицированной формы. Во всех случаях выбросы ПХ и крутизна ската были меньше у модифицированной формы, как и отдача возле частоты резонанса. Хотя в частотной области это и недостаток, АЧХ становится не плоской, но ЗЯ с добротностью Q_tс =1 и больше всегда имеют пик возле резонанса и всегда показывают плохие свойства на импульсе. Добавление ПАС в подобные системы может значительно улучшить их частотные и временнЫе характеристики.

Передаточная функция системы с ПАС имеет три степени свободы, Q_tс, Q_ts, @_lc, в соответствии с добротностью динамика в свободном поле, объёмом ящика и потерями на негерметичность. Полный анализ системы возможен благодаря технике симуляции ПХ. Поскольку на практике @_lc ограничено снизу величиной 1,0 , а системы с Q_tс< 1, которые требуется дополнительно демпфировать, могут быть в общем случае улучшены плотным наполнением ЗПМ-ом, здесь будут рассмотрены лишь ситуации, когда применение ПАС приносит существенные выгоды.

(Комментарий 20. По-нашему: если у Вас получился ЗЯ с добротностью под единицу – не спешите его дырявить! «Напихайте в него пяткой» (С) синтепон или другой ЗПМ, контролируя добротность и частоту резонанса. В большинстве случаев счастье гарантировано.)

Ниже будут рассмотрены некоторые общие примеры таких ситуаций.

1. Переход к акустическому подвесу.

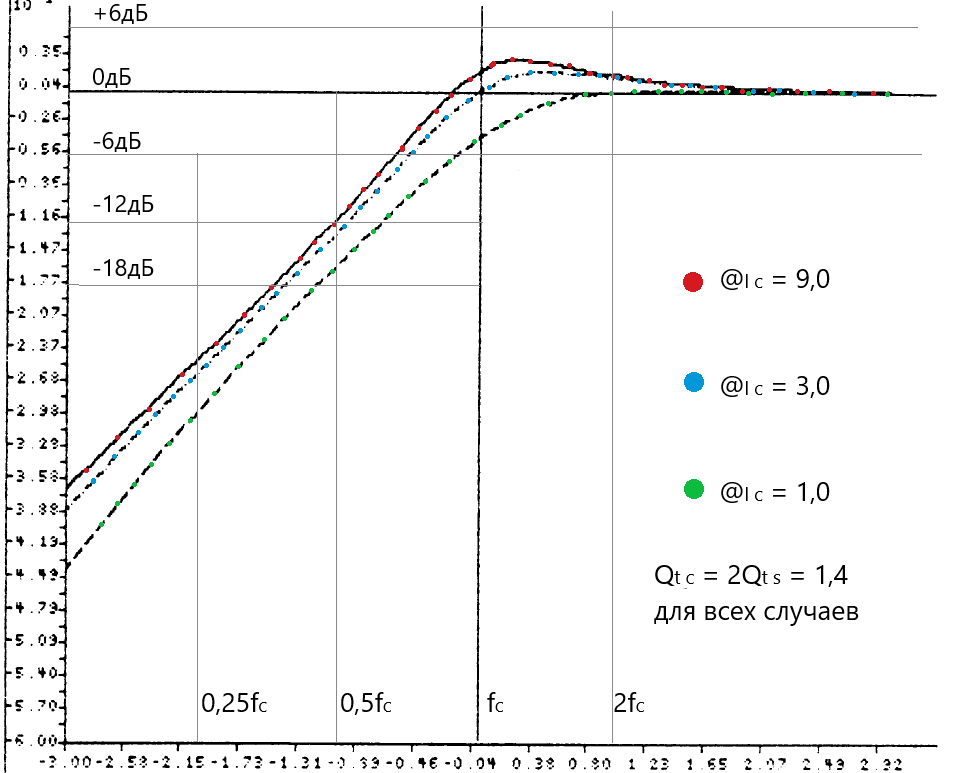
Даннаяситуациявозникает, когда Q_tc = 2Q_ts, и мы переходим к работе при & = C_as/C_ab = V_as/V_ab = 3,0. Это можно интерпретировать как уменьшение полной гибкости в 4 раза. В общем, системы с Q_tc> 2Q_ts могли бы быть более выгодными, чем бОльшие по объёму ЗЯ, при применении ПАС, но это не всегда возможно.

Рисунки ниже иллюстрируют АЧХ и ПХ для Q_tc = 2Q_ts = 1,4 и трёх разных значений @_lc: 9,0; 3,0; 1,0. Разница между значением 9,0 и безконечностью незначительна как в частотной, так и во временнОй области. Большинство реальных систем, как бы хорошо их ни конструировали, имеют небольшие щелевые потери. @_lc = 9,0 есть приблизительное представление таких потерь.

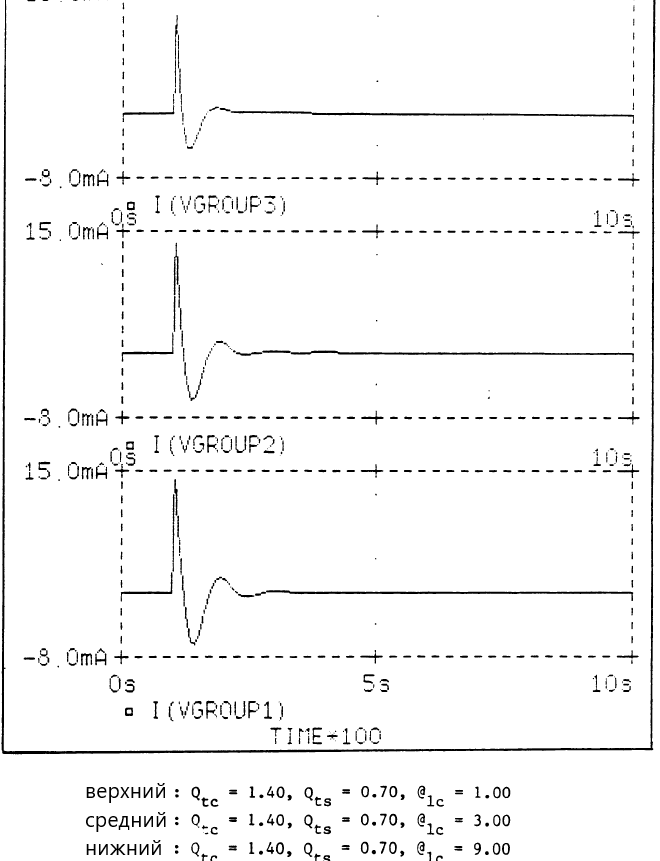
Наиболее важной особенностью является уменьшение нежелательного пика возле резонанса при @_lc = 3,0 и почти полное его исчезновение при @_lc = 1,0 , в то время как крутизна ската ниже резонанса изменилась не сильно, находясь между 12 и 15 дБ/октаву. Для варианта @_lc = 1,0 имеем маленькое поднятие АЧХ (около 0,5 дБ) на удвоенной частоте резонанса, в то время как на частоте резонанса отдача -3,5 дБ. Сравнение АЧХ данного варианта с АЧХ ЗЯ показывает, что он похож на ЗЯ с Q_tc = 0,7. Анализ ПХ показывает, что система слегка хуже демпфирована, чем ЗЯ с Q_tc = 0,7, ближе к Q_tc = 0,8. Результаты варианта с @_lc = 3,0 , АЧХ которого близка к АЧХ ЗЯ с Q_tc = 1,0 , по ПХ близки к ЗЯ с Q_tc = 1,1. В обоих случаях АЧХ и ПХ значительно лучше, чем у исходного ЗЯ.

(Комментарий 21. Автор слегка привирает. По ПХ вариант с @_lc = 1,0 ближе к ЗЯ с Q_tc = 0,9 , а вариант с @_lc = 3,0 –близок к ЗЯ с Q_tc = 1,2. Но всё равно неплохо. Так же видно, что оптимальный ЗЯ имеет лучшую ПХ и АЧХ, чем уменьшенный ЗЯ с ПАС. Фокус не удался.)

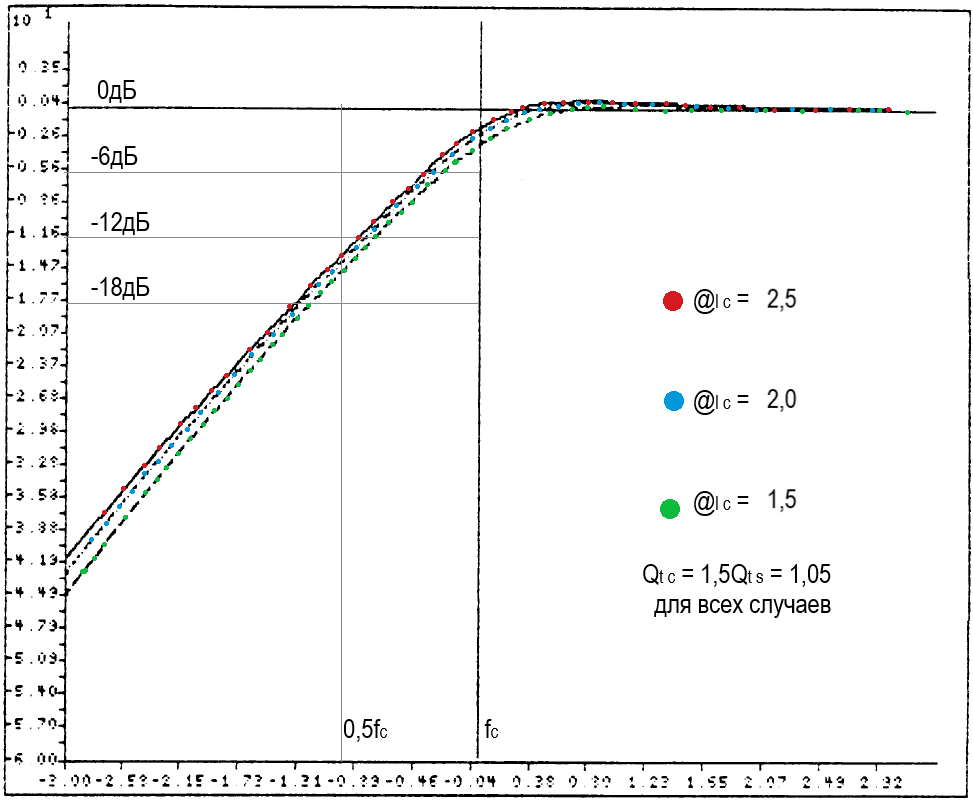
2. Система с Q_tc = 1,5Q_ts

Эта ситуация более распространена, чем предыдущая, и представлена достаточно большим числом недорогих АС типа ЗЯ, каки большим числом конусных среднечастотных динамиков, которым требуется работать вблизи частоты резонанса системы в своём отдельном боксе. Результаты наведены ниже.

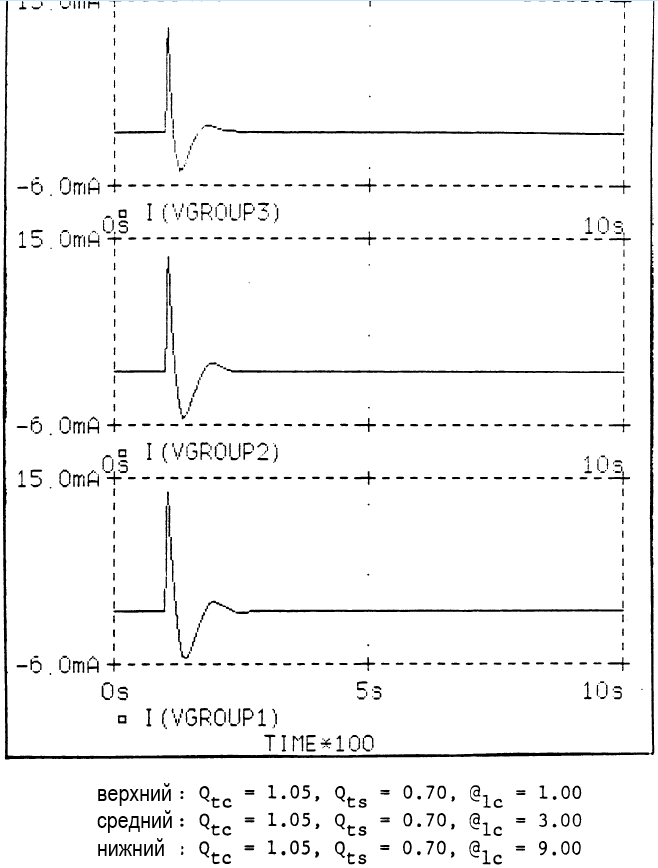
ПХ системы улучшилась во всех случаях, но в случае с @_lc = 1,0 АЧХ имеет -6 дБ на резонансе. Однако, система получила возможность точной настройки параметром R_al. Это легко осуществляется изменением количества резистивной набивки в корзине вариовента, и, хотя результаты не драматически отличаются от предыдущих, они позволяют конструктору оптимизировать систему. Например, система с @_lc = 2,0 имеет АЧХ, как у ЗЯ с Q_tc = 0,7 ,и ПХ, как у ЗЯ с Q_tc = 0,8. Что значительно лучше, чем исходный ЗЯ (Q_tc = 1,05), и система теперь имеет характеристики, подобные таковым для чистого драйвера, хотя и с более высокой резонансной частотой.

3. Система с динамиком с высокой Q_ts.

Хотя современные НЧ драйверы редко имеют Q_ts>1,0 , это не касается многих небольших конических и купольных среднечастотных драйверов. Приведенный выше анализ справедлив для длин волн, меньших(?) окружности драйвера, независимо от того, какова эта окружность, поэтому можно применить метод ПАС (pressurerelief).

(Комментарий 22. По смыслу: больших окружности драйвера, описка. Для справки: у купольного СЧ драйвера с диаметром купола 50 мм длина окружности излучателя соответствует длине волны для частоты 1100 Гц.)

Рассмотрим случай, когда Q_ts = 1,3 в системе с Q_tc = 1,7. Случай можно интерпретировать как применение средне- (или высоко-) частотного купольного драйвера в маленьком отдельном боксе. АЧХ и ПХ приведены ниже.

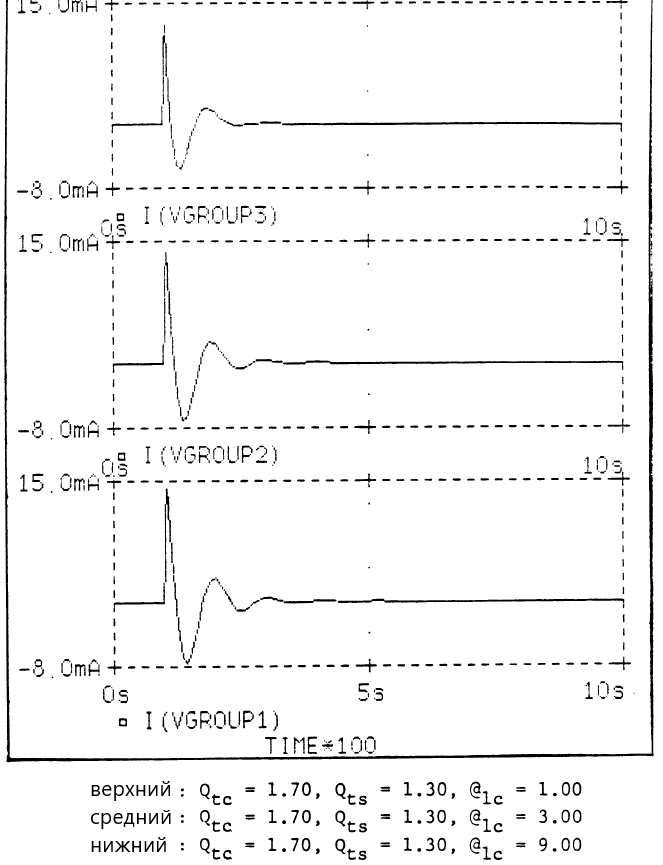
Для данного случая, при низком значении @_lc, АЧХ драматично улучшается, словно динамик стал намного более качественным. ПХ всё ещё далека от идеала, но при @_lc = 1 АЧХ почти плоская. Тем не менее, если использовать этот динамик в диапазоне средних частот (СЧ), то плоская АЧХ возле резонанса обеспечит гораздо лучшее качество, чем чистый ЗЯ, поскольку полоса СЧ обычно разделяется от полосы НЧ где-то в этой области частот. Любые пики АЧХ на СЧ приведут к искажению суммарной АЧХ системы

Крутизна ската ниже резонанса

Внимательный анализ АЧХ при низком значении @_lc показывает, что наклон ската больше, чем 12 дБ/октаву, и при приближении Q_ts к Q_tcдостигает 18 дБ/октаву. Хотя это является недостатком, сравнение с АЧХ ЗЯ при высокой Q_tc показывает, что последние также имеют 18 дБ/октаву чуть ниже резонанса. При точном рассмотрении системы ЗЯ имеют преимущество по отдаче перед ЗЯ с ПАС в области частот, где их отдача как минимум на 12дб ниже средней, потому это преимущество несущественно.

Точная настройка системы

Небольшие изменения @_lc приводят к изменению АЧХ на один-два децибелла без больших изменений в ПХ. Наиболее простой метод изменения @_lc – изменение количества слоёв ткани в корзине вариовента. Результаты хорошо видны по АЧХ или кривой импеданса. Точная настройка ЗЯ требует вскрытия ящика и добавления внутрь кусков древесины для регулировки объёма. Для ПАС регулировка выполняется без снятия драйвера или стенок ящика. Такая точная настройка необходима для точного совпадения характеристик пары динамиков.

Использование ПАС в реальной системе

Данная работа была изначально предпринята для улучшения характеристикуже существующих АС, и данный раздел является результатом применения полученных результатов.

…

Мидбасовый динамик диаметром 17 см должен перекрывать полосу 100…3200 Гц, частоты раздела будут 200 и 1600 Гц с крутизной 6 дБ/октаву. Допустимое отклонение АЧХ от линейной ±3 дБ.

Измеренные параметры в свободном поле:

Другие параметры:

Ожидаемый пик АЧХ равен +5,5 дБ на частоте 127 Гц. Реально измеренный равен +6 +/-1 дБ.

Даже с учётом затухания разделительно фильтра, уровень пика – на уровне отдачи НЧ полосы, что исказит АЧХ. Работа с передаточной функцией ЗЯ с ПАС показала, что удовлетворительные результаты могут быть получены при 1,0 <@_lc<1,5:

В ЗЯ было вырезано отверстие и вставлен вариовент от «Динаудио», тип «мягкий» (soft). Активное демпфирование изменялось добавлением слоёв фетра и пористой пены к подушечке из скреплённых волокон дакрона. Все демпфирующие материалы плотно засовывались в вариовент с максимальным сохранением их формы. При трёх слоях фетра в вариовенте было получено @_lc = 1,15 , а при четырёх – @_lc = 1,68. В законченной системе было применено три слоя. Результирующая АЧХ показана ниже.

Пик АЧХ +1,2 дБ на частоте около 140 Гц. Попытка сделать @_lc меньше 1,15 приводила к искажению фазовой характеристики и очень несимметричной кривой импеданса, что показывает присутствие взаимодействия акустической массы в вариовенте с гибкостью оформления ЗЯ, чего следует избегать (см. приложение Б).

Второй динамик из пары имел следующие параметры:

Симуляция показала, что @_lc = 1,4 приведёт к совпадению АЧХ с первой в пределах 0,5 дБ. При работе с вариовентом было получено @_lc = 1,37.

…

Измеренные АЧХ пары приведены ниже.

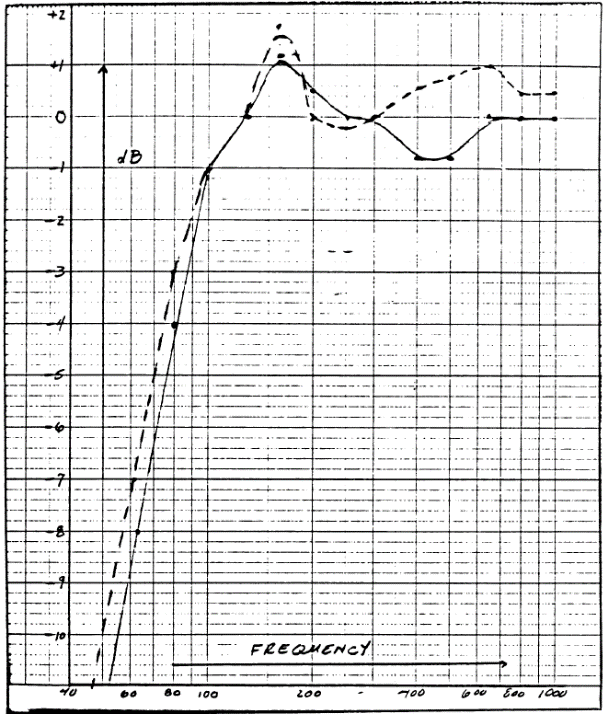
Отклонения в паре в пределах 1 дБ, инструментальной погрешности измерения.

На рисунке ниже наведены расчётные ПХ для ЗЯ и пары ЗЯ с ПАС.

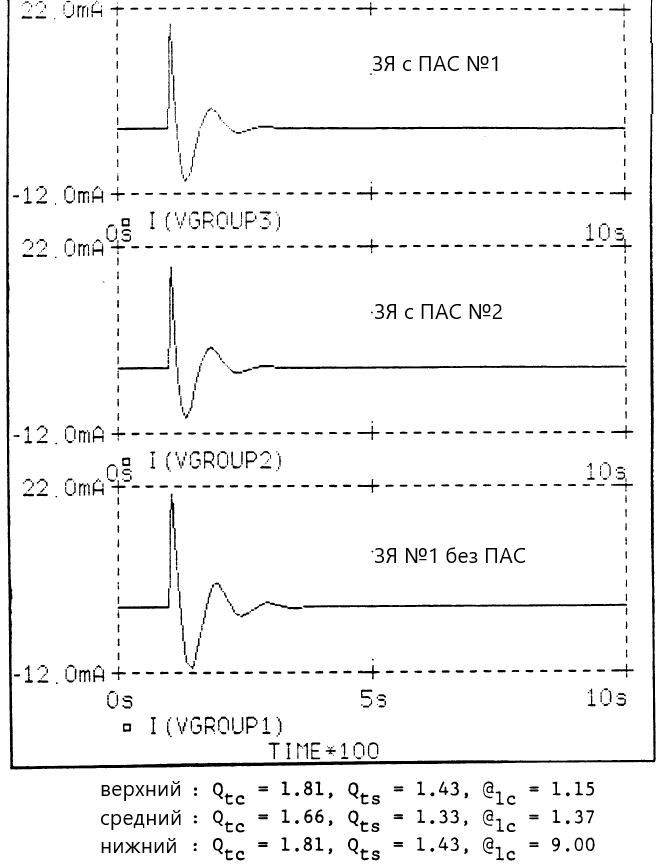
Расчётная ПХ далека от идеала, но входной сигнал будет ослаблен ниже 200 Гц, и затухающие колебания уменьшатся по амплитуде. Хотя это не было проверено на слух, но ЗЯ с ПАС имеет значительно лучшие характеристики, чем исходный ЗЯ.

Законченная система имеет все преимущества конфигурации ПАС. 17-см драйвер, который был почти неприменим в ЗЯ, показал отличную АЧХ после оптимального апериодического демпфирования. Совпадение АЧХ в паре в пределах ±0,5 дБ приведёт к стойкости ширины и глубины звуковых образов.

(Комментарий 23. Автор дважды привирает. Во-первых, ПХ вышла никудышняя. Предварительно следовало забить ЗПМ все 12 литров объёма, а потом ставить ПАС. Во-вторых, какие ширина и глубина звукового образа при частоте сигнала 100…200 Гц, когда и стереоэффекта нет? А выше динамики и так были идентичны.)

Подведение итогов

Сравнительная характеристика ЗЯ и ЗЯ с ПАС наведена ниже. Предполагается, что системы имеют Q_tc>1,0 , при которой ПАС даёт выигрыш. В каждой категории применение ПАС показывает отменные результаты.

Категория	Закрытый ящик	ЗЯ с ПАС
АЧХ	пик из-за недемпфированного резонанса	контролируется благодаря дополнительному демпфированию
ПХ	плохая из-за недемпфированного резонанса	контролируется благодаря дополнительному демпфированию
Крутизна ската	>12 дБ/окт сразу ниже резонанса, дальше 12 дБ/окт	>12 дБ/окт
Подгонка пары	сложно, через изменение объёма ящика	легко выполнить без вскрытия ящика

Часть 6. Заключение

…

Хотя система ЗЯ+ПАС более сложна, чем просто ЗЯ, внедрение ПАС в большинстве существующих систем типа ЗЯ, требующих дополнительного улучшения демпфирования и/или АЧХ, не представляет сложности. Тем более, что изменение фактора потерь @_lc на 25% незначительно влияет на вид ПХ. Влияние на АЧХ вблизи резонанса значительно сильнее. Выручает то, что требования к величине @_lc, основанные на требуемой АЧХ и требуемой ПХ, примерно совпадают. Например, система с высокой Q_tc требует низкого значения @_lc для коррекции её ПХ; одновременно пик АЧХ из-за высокой Q_tc также уменьшается при низком значении @_lc. Система с низкой Q_tc (Q_tc около 1,0) не требует столь мощного дополнительного демпфирования, поэтому  слишком низкое значение @_lc не нужно. Таким образом, получим и не очень значительное отклонение АЧХ от плоской.

…

Улучшенная АЧХ и хорошо контролируемый переходной процесс позволяют конструктору создавать физически небольшие системы, cохраняя преимущества бОльших ящиков, точно настраивать существующие системы, улучшать свойства низко-, средне- и, возможно, высокочастотных блоков. Это представляет существенное дополнение к существующей теории конструирования АС.

…

Приложение А. Измерения (пропущено)

Приложение Б. Взаимодействие гибкости оформления с акустической массой в вариовенте

Поскольку в отверстии вариовента есть масса воздуха M_av, может произойти второй резонанс системы на частоте

w_b² = 1/(C_abM_av).                                                                           (Б1)

Это то свойство, которое даёт преимущество конструкции с фазоинвертором (ФИ), но в системе с ПАС это недопустимо. Вариовент заполнен ЗПМ, имеющим высокое внутреннее поглощение. Поток воздуха через вариовент не ламинарен, воздух вынужден двигаться через «тоннели» сквозь ЗПМ. Это очень увеличивает инерцию воздуха, попавшего в вариовент, и, в результате, очень увеличивает акустическую массу. В результате частота резонанса ящик/отверстие получается очень низкой, и она очень хорошо демпфируется.

Во всех системах, измеренных в данной статье, этот второй резонанс появлялся только у ПАС, которые были почти без демпфирующего материала. На кривой импеданса появлялся второй горб. Поскольку измерения проводились в диапазоне полных двух октав ниже резонанса, и в хорошо демпфированном отверстии второй горб никогда не появлялся, то вариовент должен иметь почти безконечнуюакустическую массу. Тогда потери в хорошо демпфированной ПАС чисто резистивные, а система – апериодически демпфирована.

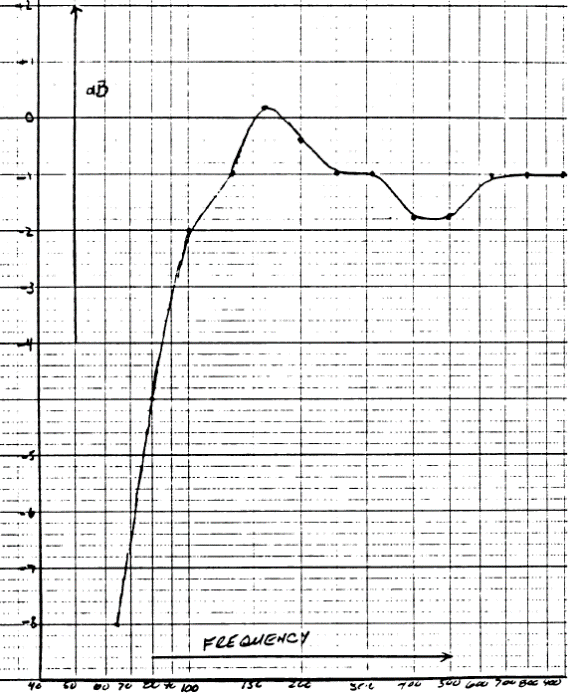
Если же демпфирование в отверстии недостаточно, кривая импеданса системы приобретёт следующий вид, с явно видимым вторым горбом (нижняя кривая):

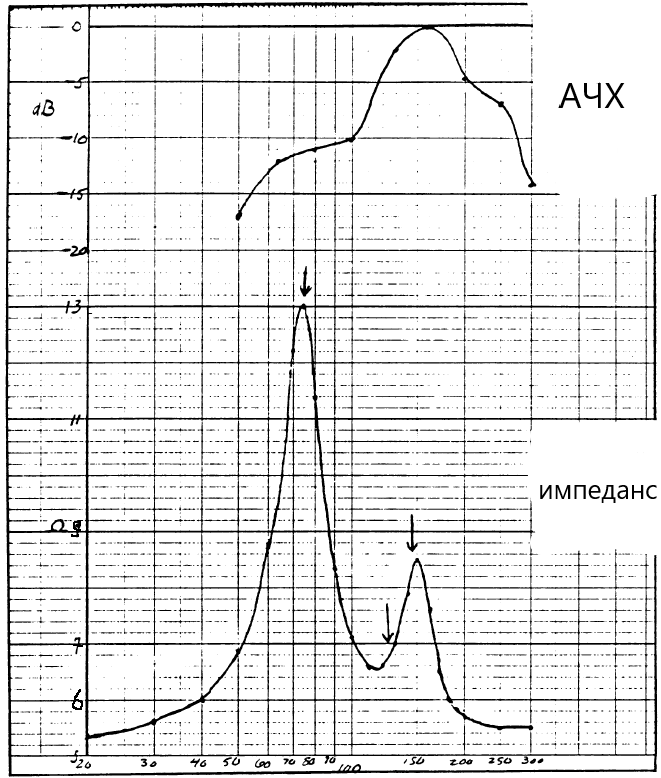
Это случилось, когда 17-см драйвер работал с вариовентом, в котором был только блок волокон дакрона, без фетра. Соответствующая АЧХ приведена вверху рисунка, масштаб по вертикали 5 дБ/клеточка. Пик АЧХ имеет значение +10 дБ на частоте 130 Гц (вместо +6 дБ при 127 Гц в исходном ЗЯ), а спад ниже частоты верхнего резонанса не имеет ровных участков. Субъективно, мидбасовое звучание состоит из одной основной ноты, а ПХ – крайне плохая. Такое допускатьнельзя.

Приложение В. Характеристики ЗЯ (пропущено)

(Комментарий 24. Не хотел играться с картинками ужасного качества.)

* * * * *

Сделаем общие выводы по статье.

1. ПАС является мощным инструментом влияния на характеристики ЗЯ.
2. Влияние ПАС на АЧХ значительно сильнее, чем на ПХ.
3. ПАС оправдана при полной добротности динамика в ЗЯ больше 1,0.
4. При полной добротности динамика в ЗЯ меньше 1,0 показано заполнение объёма ящика ЗПМ-ом.
5. В статье не рассмотрен вариант одновременного заполнения объёма ящика ЗПМ-ом и применения ПАС, в тяжёлых случаях. Вероятно, из-за большого повышения затрат времени и материала при исследовании и настройке.
6. Существенного улучшения ПХ при применении ПАС совместно с динамиком с высокой Q_tsне замечено. Только улучшение АЧХ.
7. Улучшение АЧХ и ПХ динамиков с низкой собственной добротностью Q_ts – почти до уровня ПХ динамика в безконечном экране, ценой повышения резонансной и нижней рабочей частоты динамика.
8. Существуют сочетания параметров системы с ПАС, при которых АЧХ и ПХ ухудшаются, из-за резонанса ящик/отверстие.
9. При прочих равных, АЧХ и ПХ ЗЯ с добротностью Q_tс = 0,5…0,8 всегда лучше, чем у ЗЯ с ПАС в ящике меньшего объёма (оба варианта – без заполнения ЗПМ). Природу надуть не удалось. Оптимальность диапазона Q_tс = 0,5…0,8 для ЗЯ требует дополнительного исследования.

Автор: Николай Марков