Статья написана по мотивам статей (их желательно прочесть загодя):
Рассмотрим работу динамического громкоговорителя (дальше – динамика) от источника тока, управляемого напряжением (ИТУН). Будем называть такой режим работы токовым.
Звуковой сигнал на выходе усилителя мощности (УМ) представляет собой переменное напряжение. Но сила, движущая звуковую катушку (ЗК), пропорциональна току. Рассмотрим формулу для силы, движущей ЗК:
F = BL · I (1), где
BL – произведение индукции в зазоре на длину провода в зазоре;
I – ток в ЗК.
Разбираемся с током в ЗК, о BL скажем пару слов в конце. Преобразование подводимого напряжения в ток происходит на комплексном сопротивлении динамика. Оно, в свою очередь, имеет активную (сопротивление ЗК, приведённые сопротивления излучения и потерь на токи Фуко) и реактивную (индуктивность ЗК, параллельный контур на частоте механического резонанса) составляющую. В режиме малого сигнала, когда амплитуда смещения и выделение тепла незначительны, разговор о преимуществах работы динамика от ИТУН перед обычным включением (от источника напряжения, УМ с Rвых ≈ 0) лишён смысла. Поэтому в дальнейшем рассматриваем работу при значительном смещении ЗК. Если выходное сопротивление ИТУН значительно выше, чем максимальный импеданс в рабочей полосе частот, то девиации ни активной, ни реактивной составляющей импеданса, вызванные нагревом и смещением ЗК, не приведут к появлению ошибки (искажений) при преобразовании напряжение/ток. Превосходно. Но, почитав [1] и [2], приходим к выводу, что получить ВСЕ бонусы от токового режима работы можно лишь в схеме полного би- или, что лучше, триампинга с активными кроссоверами и активными компенсирующими цепями. Причем УМ НЧ звена целесообразно делать обычным, с Rвых≈0, чтобы частота, на которой реактивное сопротивление ЗК становится равным сумме активного сопротивления ЗК и выходного активного сопротивления источника, была не ниже максимальной рабочей частоты динамика в конкретном устройстве (речь о частоте среза «встроенных фильтров», см. [1]).
Оценим корректность данной рекомендации. При режиме работы от источника напряжения, в предположении ΔLзк / Lзк = const (позже покажем, что ΔLзк / Lзк ≠ const но пока что так), ток через ЗК на частотах выше электромеханического резонанса:
I = U / √ ( R2 + (ω · (Lзк + ΔLзк))2) (2), где
- Lзк – индуктивность ЗК;
- ΔLзк – девиация Lзк, вызванная смещением ЗК от положения равновесия;
- R – полное активное сопротивление ЗК.
При R << Ι ωLзк Ι имеем девиацию тока в ЗК ΔI, пропорциональную ΔLзк:
ΔI ∝ ΔLзк.
Это теоретический максимум искажений на очень высокой частоте ω.
При R = Ι ωLзк Ι имеем ΔI ∝ ΔLзк/2. Это рекомендация из [1], искажения вдвое меньше максимально возможных, под ω подразумеваем максимальную рабочую частоту. Напомню, что в R, кроме активного сопротивления ЗК, входят активные приведённые сопротивление излучения и потерь от токов Фуко. Но в [1] оперируют лишь с активным сопротивлением ЗК.
При R = 2 · Ι ωLзк Ι имеем ΔI ∝ ΔLзк/5
При R = 3 · Ι ωLзк Ι имеем ΔI ∝ ΔLзк/10 и так далее.
В общем случае искажения, вызванные ΔLзк, уменьшаются в k раз (и на низких частотах несущественны):
k = 1 + R2 / ZLзк2 (3)
В таком случае рабочая версия рекомендации звучит так:
Для эффективного снижения искажений от ΔLзк сумма активного выходного сопротивления источника сигнала + активного сопротивления ЗК должна более чем в 2-3 раза превышать импеданс индуктивности ЗК на максимальной рабочей частоте.
Под максимальной рабочей частотой динамика в устройстве следует понимать частоту раздела сверху для НЧ или 20 кГц для ШП/ВЧ головок.
Обратите внимание, что причиной искажений от ΔLзк является смещение диффузора под действием тока низкой частоты, а сами искажения появляются на средних частотах и нарастают на высоких частотах! Поскольку ΔLзк изменяется в пределах ±ΔLзк по закону тока низкой частоты, то возникнет амплитудная модуляция более высокочастотных составляющих низкочастотными, искажения на СЧ и ВЧ будут интермодуляционными (ИИ).
Глядя на (3), некорректно говорить о токовом режиме, когда АС подключена к УМ с выходным сопротивлением, скажем, 5 Ом, как это имеет место в [2]. На практике «токовый режим» (именно так, в кавычках!) часто сводится к подбору значения выходного сопротивления УМ, работающего на АС с фильтром, построенным для работы от источника напряжения. Субъективное улучшение звучания при работе от УМ с Rвых в несколько Ом следует отнести исключительно к изменению тембрального баланса АС, фильтр которых рассчитан исходя из RвыхУМ≈0. Для ЗЯ/ОЯ/вариовента, независимо от схемы фильтра, увеличение Rвых источника сигнала приводит к подъёму самых низких частот. Для оформлений ФИ/ПИ подъём НЧ будет иметь место на двух частотах максимумов импеданса. Добавка на частоте верхнего пика сходна с таковой для ЗЯ, с той разницей, что у ФИ/ПИ этот горб появится чуть выше по частоте и будет значительно круче обрываться в сторону низких частот. Добавка же на частоте нижнего пика приведёт лишь к увеличению амплитуды диффузора и резкому росту искажений НЧ динамика. Таким образом, ФИ/ПИ более критичен к завышенному Rвых УМ. Впрочем, это общеизвестно! 😊
Попытка использовать в модели и расчётах простейшую схему замещения динамика (как в [1]) – один резистор R и одну катушку Lзк – потерпела фиаско. Слишком велики изменения реального активного сопротивления ЗК Rа и реальной Lзк в рабочем диапазоне частот. Кроме того, с ростом частоты значение ΔLзк уменьшается медленнее, чем Lзк, и их отношение растёт. Попробую физически и лирически описать ситуацию. Ниже представлен рисунок, справедливый для многих динамиков, у которых длина ЗК больше высоты воздушного зазора:
Рис.1 Политика апартеида витков по признаку положения относительно зазора
ЗК условно разделена на три цветных части. Виток, находящийся в зазоре (зелёный), имеет бОльшую индуктивность на НЧ и одновременно бОльшие потери на токи Фуко на СЧ/ВЧ, чем виток, находящийся вне зазора, поскольку первый находится в непосредственной близости от ферромагнетика с обеих сторон. Индуктивность (и токи Фуко) «внезазорных» витков, находящихся выше зазора, где нет керна (красные), значительно меньше, чем у «зазорных». Витки, находящиеся ниже зазора (жёлтые), имеют промежуточные значения индуктивности и потерь на токи Фуко, ближе к зелёным. При смещении ЗК количество, индуктивность и потери на токи Фуко зелёных витков не изменяются (вылет ЗК из зазора не рассматриваем 😊), но перераспределяется количество красных и жёлтых. Следовательно, за появление ΔLзк отвечают витки, НЕ находящиеся в зазоре. Сразу вопрос: можно ли уменьшить ΔLзк конструктивно? Можно, если минимизировать отличия в условиях работы красных и жёлтых, сделав керн вровень с верхним краем ЗК. Другой способ, похуже: керн в виде гриба, жёлтые находятся дальше от ферромагнетика. Третий способ: длина ЗК меньше высоты зазора с запасом на ход, красных и жёлтых нет в принципе (андерханг) Поскольку значение индукции В для всех витков ЗК-андерханга почти константа (они все зелёные), то в правой части равенства (1) вообще нет нелинейностей, и андерханг следует признать прорывным методом устранения искажений. К сожалению, этот способ неприменим к НЧ динамикам. Представьте себе НЧ динамик с магнитной системой типа андерханг, в которой длина ЗК равна 22 мм, а линейный ход равен 6 мм. Тогда высота воздушного зазора должна быть больше 34 мм. Для сравнения: у 75ГДН-1-4 длина ЗК такая же – 22 мм, высота зазора 10 мм, линейный ход – те же 6 мм (грубо). При равных диаметрах ЗК для одинаковой индукции в зазоре первая система потребует магнит более чем в 3,4 раза мощнее, чем у 75ГДН (о насыщении керна молчу). Кардинально решает проблему светофора полностью симметричная система из двух встречных идентичных магнитных систем и двух ЗК, соединённых с одним диффузором.
Рассмотрим схему замещения динамика 10ГД-30. Площади цветной заливки внутри эллипсов приблизительно соответствуют вкладу разных групп витков в каждую из индуктивностей:
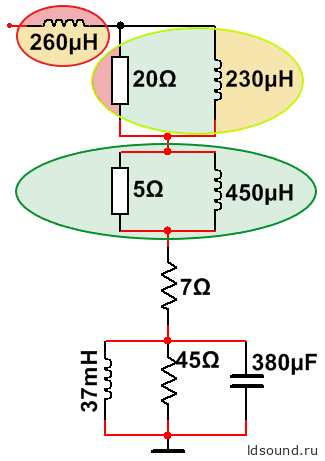
Рис.2 Приблизительное соответствие разных групп витков ЗК элементам схемы замещения динамика.
С увеличением частоты значение Lзк снижается, активное сопротивление Ra – растёт, поскольку две из трёх индуктивностей всё больше шунтируются сопротивлениями, а ΔLзк почти не изменяется: основная часть ΔLзк соотносится с красными, имеющими минимальные потери на токи Фуко. Для наихудшего случая можно принять, что с ростом частоты не уменьшается вовсе, ΔLзк=const. А что же активное сопротивление? Оно также будет плавать из-за изменений потерь от токов Фуко, но по другому закону! Сложная задачка получается. Равенство (2) принимает вид:
I = U / √ (R + ΔR)2 + (ω · (Lзк + ΔLзк))2 (4)
Задача. Динамик 10ГД-30 работает от источника с Rвых=0 Ом. Найти частоту Fгр, на которой искажения, вызванные ΔLзк, уменьшаются вдвое относительно теоретического максимума, и частоту F+, на которой уменьшение составит 10 раз, для случаев ΔLзк/Lзк=const и ΔLзк=const. Примем, что вносимые ΔLзк и ΔR не изменяют ФЧХ импеданса динамика. Искажения от ΔR не рассматриваем (пока).
Решение. Для случая ΔLзк/Lзк=const воспользуемся равенством (3). Нужны графики модуля и фазы входного импеданса 10ГД-30:
Рис.3 Модуль и фаза входного импеданса динамика 10ГД-30
(Для удобства я использую графики, полученные при симуляции схемы замещения. Используйте реально снятые графики). По графикам рассчитываем зависимость активного и индуктивного сопротивления от частоты:
Ra = ΙZΙ · cosφ, ZLзк = ΙZΙ · sinφ (5)
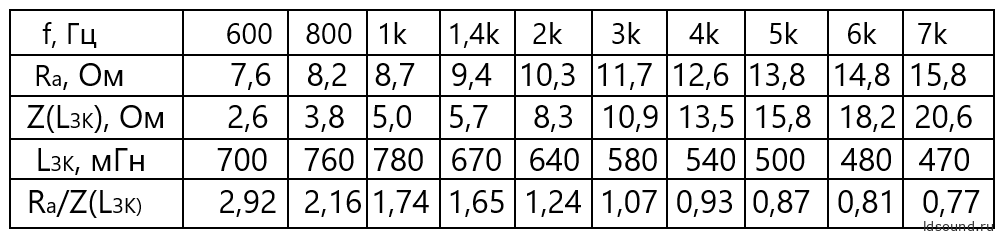
Нижняя частота для расчёта принята 600 Гц, верхняя рабочая частота 10ГД-30 по уровню -12 дБ составляет около 7 кГц. Результаты – в Таблице 1:
Таблица 1. Зависимость параметров 10ГД-30 от частоты.
Обработаем результаты. Lзк ниже 1 кГц падает – сказывается влияние механического резонанса, вносящего ёмкостную составляющую в импеданс. Благодаря токам Фуко с ростом частоты Lзк падает, а Ra – растёт. По Таблице 1 получаем: Fгр=3,5 кГц, F+=600 Гц. Для случая значения в нижней строчке Таблицы 1 для f≥1,4 кГц пересчитываю следующим образом. Значение Lзк на частоте 1,4 кГц в 670/780=1,164 раза меньше, чем максимальное (при 1 кГц), следовательно, влияние ΔLзк во столько же раз выросло. Значение 1,65, соответствующее f=1,4 кГц, заменяем на 1,65/1,164=1,42 и т.д. Получаем: Fгр=2 кГц, F+=600 Гц. Усреднённые значения: Fгр=2,7 кГц, F+=600 Гц. Для случая простейшей схемы замещения динамика были получены значения: Fгр=1,5 кГц, F+=500 Гц.
Критерий оценки частот и связан с ФЧХ импеданса:
Fгр = частоте перехода фазы импеданса через 45° (=arcsin 1) (6)
F+ =частоте перехода фазы импеданса через 20° (=arcsin 1/3) (7)
Взглянув на ФЧХ импеданса, можно уже кое-что сказать… Ниже приведены частоты F+/Fгр в предположении ΔLзк/Lзк=const для ряда динамиков по критериям (6) и (7).
- 10ГД-30 – 0,6/3,5 кГц
- 20ГДС-1-8 – 0,9/4,7 кГц
- 35ГДН-1-4 – 0,4/1,2 кГц
- 15ГД-17 – 1/20 кГц
- 75ГДН-3-4/75ГДН-1-4 – 250/>1000 Гц (фаза не достигла значения 45°)
- 15ГД-14 – 0,6/3 кГц
- 6ГД-2 – 0,55/3,5 кГц
- 6ГДШ-5-4 – 1,5/7 кГц
- SC13/8 Visaton – 1,5/12 кГц
- TW-70 – 5/20 кГц
- Tangband W8-1808–8,5/25 кГц
Если уменьшить оценки Fгр на 20-25% для усреднения со случаем ΔLзк=const, а оценки F+ уменьшить на столько же для учёта влияния ΔR, то оценки частот будут ближе к реальности. Итак, чтобы искажения 10ГД-30, связанные с ΔLзк и ΔR, были достаточно малыми при мощности, близкой к номинальной, его верхняя граничная частота не должна превышать F+≈500 Гц. Привет конструкторам 10МАС-1.
Посчитаем, как будет изменяться ΔI/ΔLзк в зависимости от частоты для динамика 10ГД-30, за 100% принят теоретический максимум влияния. Зависимость при работе от источника с Rвых=0 Ом (влияние ΔR на ток в ЗК здесь не учтено):
- ΔLзк=const – красная кривая
- Rвых= 0 Ом и ΔLзк/Lзк – оранжевая
- Rвых= 22 Ома и ΔLзк/Lзк – зелёная кривая
Рис.4 Расчетная зависимость ΔI/ΔLзк от частоты для разных исходных.
Красиво. А что скажет товарищ Мультисим?
Построим ряд зависимостей ΔI/ΔZзк для 10ГД-30 и разных фильтров, внося изменения как в индуктивную, так и в активную составляющую Zзк. Методика следующая. Создаём две заготовки схем замещения, отличающиеся номиналами трёх элементов (каждый на -10%), которые, предположительно, отвечают за изменение импеданса при смещении ЗК:
Рис.5 Создание пары заготовок схем, отличающихся номиналами трёх элементов.
Пара позволяет быстро оценить изменение ΔI/ΔZзк, вместе с АЧХ фильтра по напряжению. Изменение модуля импеданса правой схемы относительно левой составляет -7,5% на частоте 7 кГц, но я не старался получить точно -10%, модель светофора внесёт большую погрешность.
Вертикальная шкала градуирована в %, за 100% принят теоретический максимум искажений. Здесь и дальше синяя кривая – АЧХ фильтра по напряжению в процентах, красная – относительная разница токов в динамиках для двух схем замещения, умноженная на 1000, зелёная – то же, с учётом коэффициента передачи фильтра (информативная кривая).
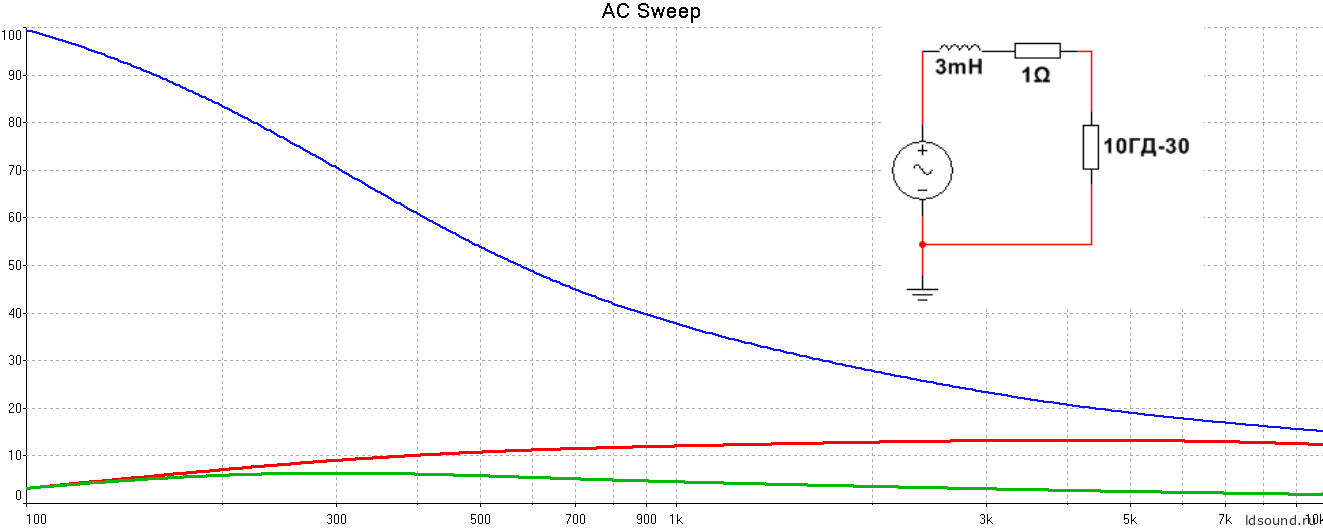
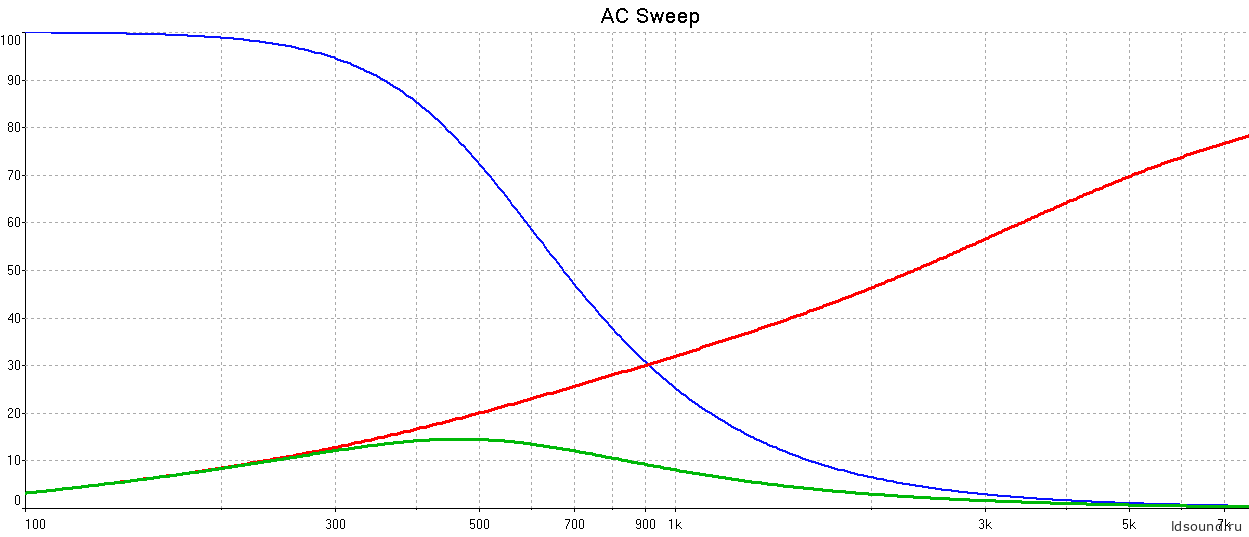
Ниже картинка при Rвых УМ=0, фильтр отсутствует:
Рис.6 Зависимость при включении от источника напряжения.
И что? Где наши F+=500 Гц и Fгр=2,7 кГц? Картина гораздо непригляднее: F+=250 Гц и Fгр=2,3 кГц! Большой привет конструкторам 10МАС.
При Rвых УМ 22 Ом, фильтр отсутствует:
Рис.7 Зависимость при включении от источника с высоким выходным сопротивлением.
Следует заметить, что при построении зелёных кривых на Рис.4 и Рис.7 не учтён подъём АЧХ, вызванный ростом импеданса 10ГД-30 выше 500 Гц. Если его компенсировать, то значение ΔI на частоте 5 кГц дополнительно уменьшится вдвое.
Разница между Рис.6 и Рис.7 доказывает эффективность токового режима работы динамика в плане уменьшения искажений, вызванных появлением ΔZзк.
Прекрасно. Смотрим влияние фильтров, ведь их выходное сопротивление вовсе не равно нулю!
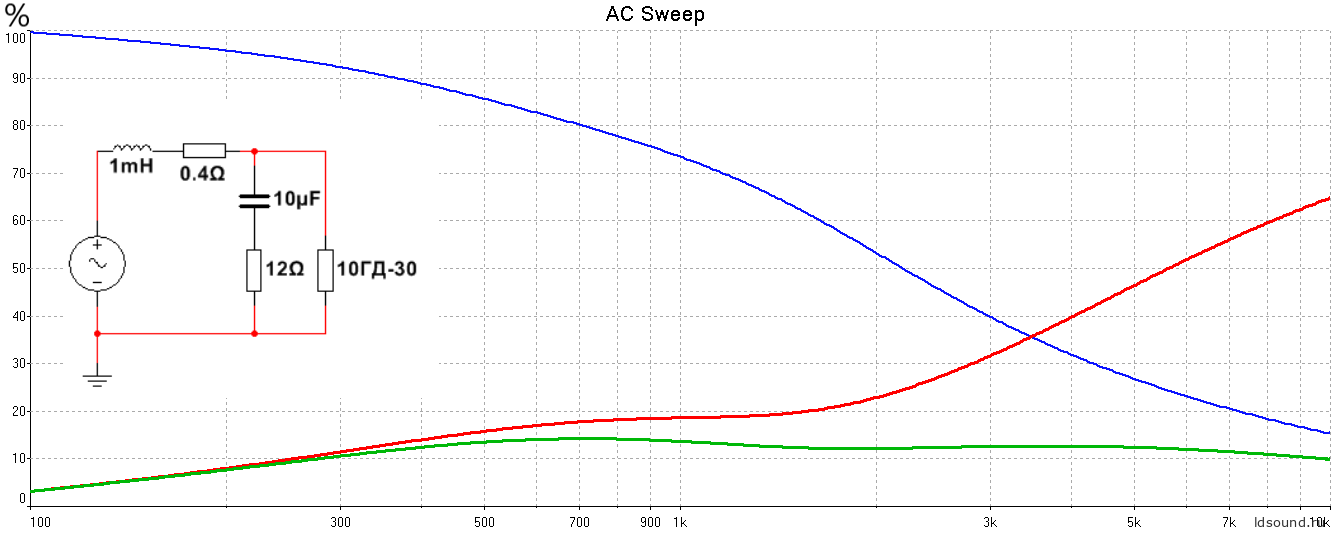
Классический первый порядок (с цепочкой Цобеля) с низкой частотой среза, раздел по уровню -6 дБ на частоте 600 Гц (здесь и дальше последовательно с катушкой ФНЧ изображено активное сопротивление катушки ФНЧ):
Рис.8 Зависимость при включении через ФНЧ с низкой частотой среза.
Первый порядок с высокой частотой среза(с цепочкой Цобеля), раздел по уровню -6 дБ на частоте 2,2 кГц:
Рис.9 Зависимость ΔI/ΔZзк при включении через ФНЧ с высокой частотой среза.
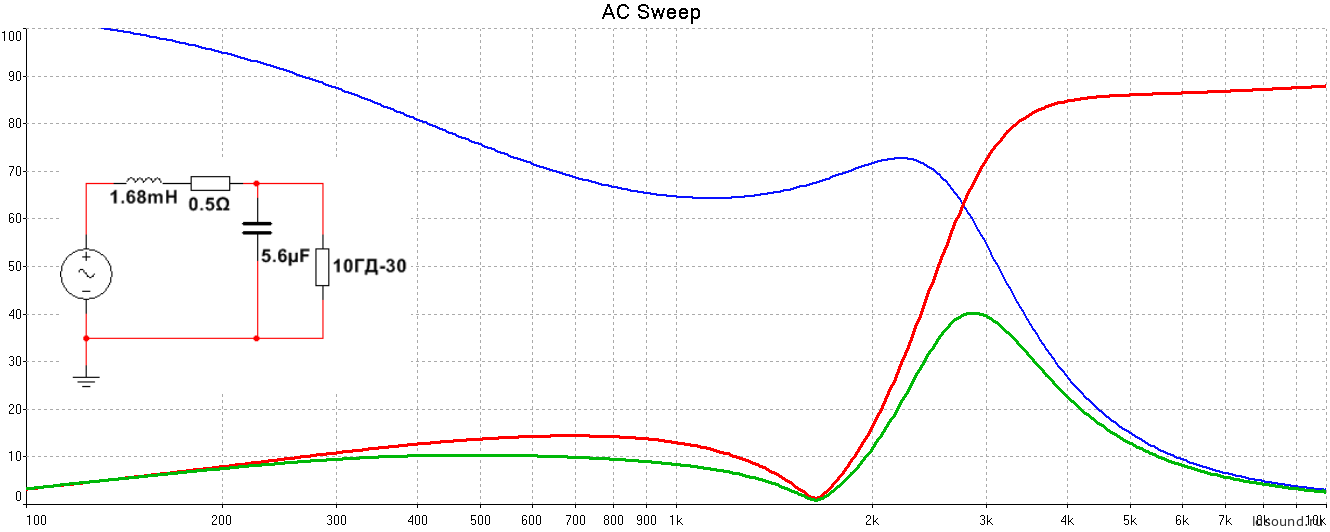
Катушка соло, без цепочки Цобеля:
Рис.10 Зависимость ΔI/ΔZзк при включении через одиночную катушку индуктивности.
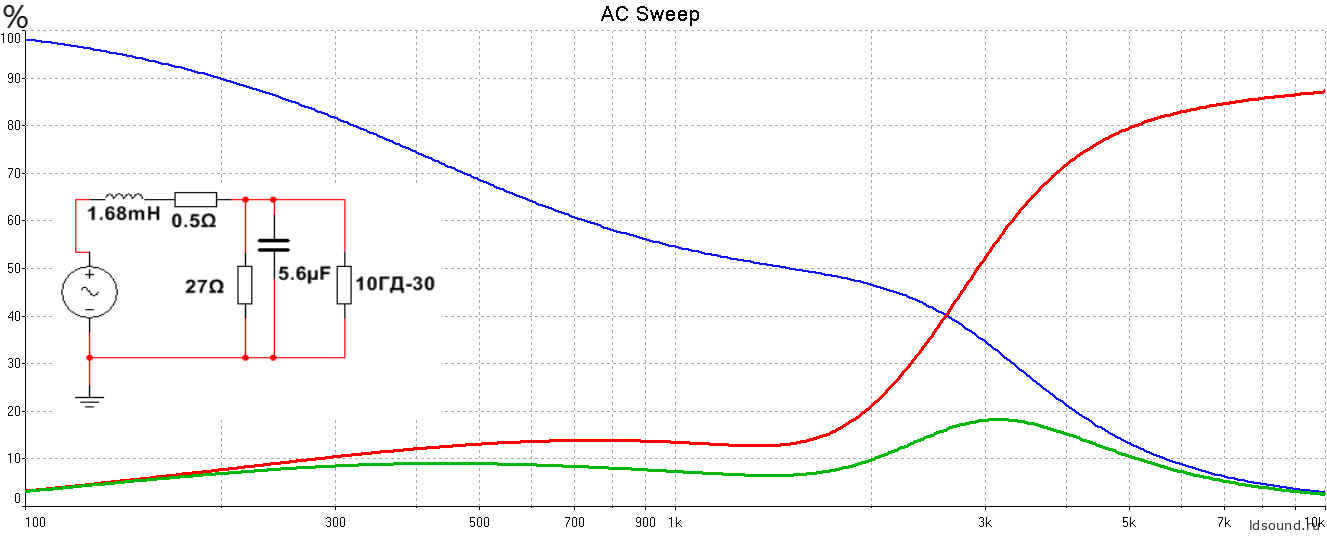
Фильтр второго порядка с низкой частотой среза, раздел по -6 дБ на частоте 650 Гц:
Рис.11 Зависимость ΔI/ΔZзк при включении через ФНЧ второго порядка.
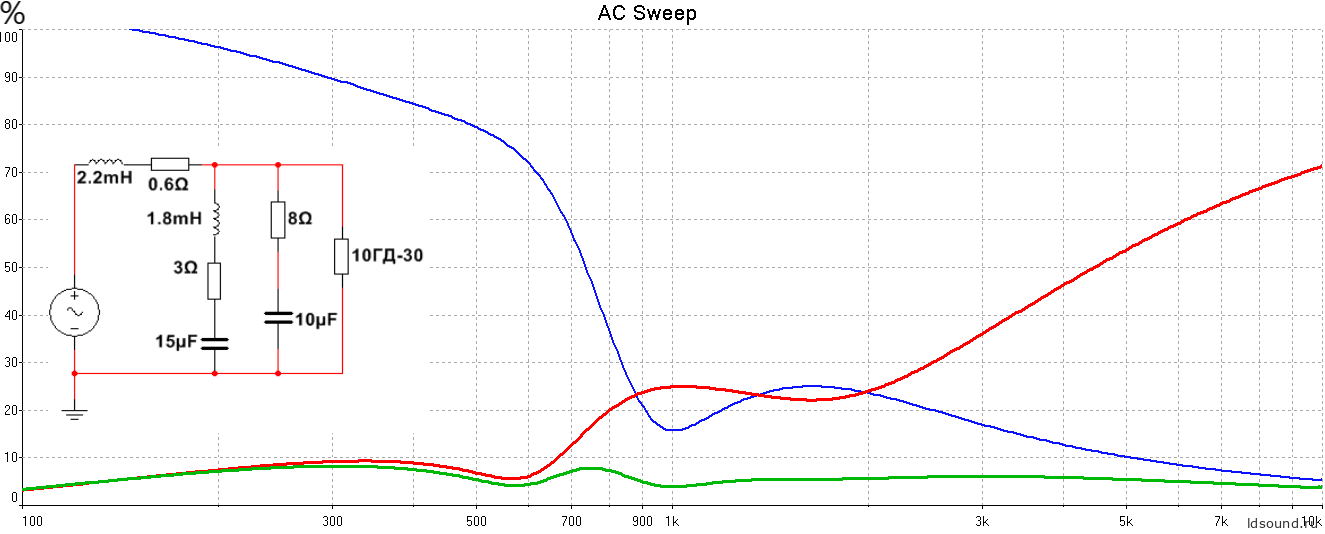
Фильтр первого порядка с режекторным последовательным фильтром, настроенным на выброс АЧХ 10ГД-30 в районе 800-1200 Гц:
Рис.12 Зависимость ΔI/ΔZзк при включении через ФНЧ с режектором.
Фильтр от А. Бокарёва: https://ldsound.club/index.php?threads/as-na-baze-10gd-30e-i-vch-visaton-tw70.1088/post-77840:
Рис.13 Зависимость ΔI/ΔZзк при включении через фильтр от А.Б.
Второй порядок с наличием выброса на АЧХ перед срезом. Фильтр от А.Б. без одной детали, или маму надо слушаться 😊:
Рис.14 Зависимость ΔI/ΔZзк при включении через неудачный ФНЧ.
По всем зависимостям в целом. Достаточно большая индуктивность последовательно с динамиком есть необходимое условие снижения влияния ΔZзк, и она же будет причиной получения низкой частоты раздела. Правда, фильтр на рис.13 создан для двухполосной АС с разделом около 2 кГц, но работает только благодаря особенностям АЧХ динамика 10ГД-30.
А что скажет вариант биампинга: активный ФНЧ второго порядка по Баттерворту с частотой среза по -3 дБ 500 Гц перед УМ в режиме ИНУН?
Рис.15 Зависимость ΔI/ΔZзк при включении от ИНУН с активным ФНЧ перед ним.
Стоит ли заморачиваться с ИТУН и строить под него пассивные фильтры, как в [1]? Конечно, нет. Или би-/триампинг ИТУН по всей строгости закона с коррекцией перед УМ, или ИНУН с нормальными пассивными фильтрами, убирающими влияние ΔZзк ниже плинтуса! В нормально сконструированной двух/трёхполосной АС на СЧ/ВЧ динамики частоты, близкие к частотам механических резонансов, приходят с уровнем, недостаточным для заметного смещения ЗК, и о влиянии ΔZзк на общий уровень искажений можно не говорить, ограничения по (6) и (7) для СЧ/ВЧ динамиков упраздняются.
Оценим ΔI/ΔZзк для 75ГДН-1-4 и разных фильтров. Методика та же: «три по -10%», значение кривых – как в примере с 10ГД-30.
Напрямую от ИНУН без ограничения полосы:
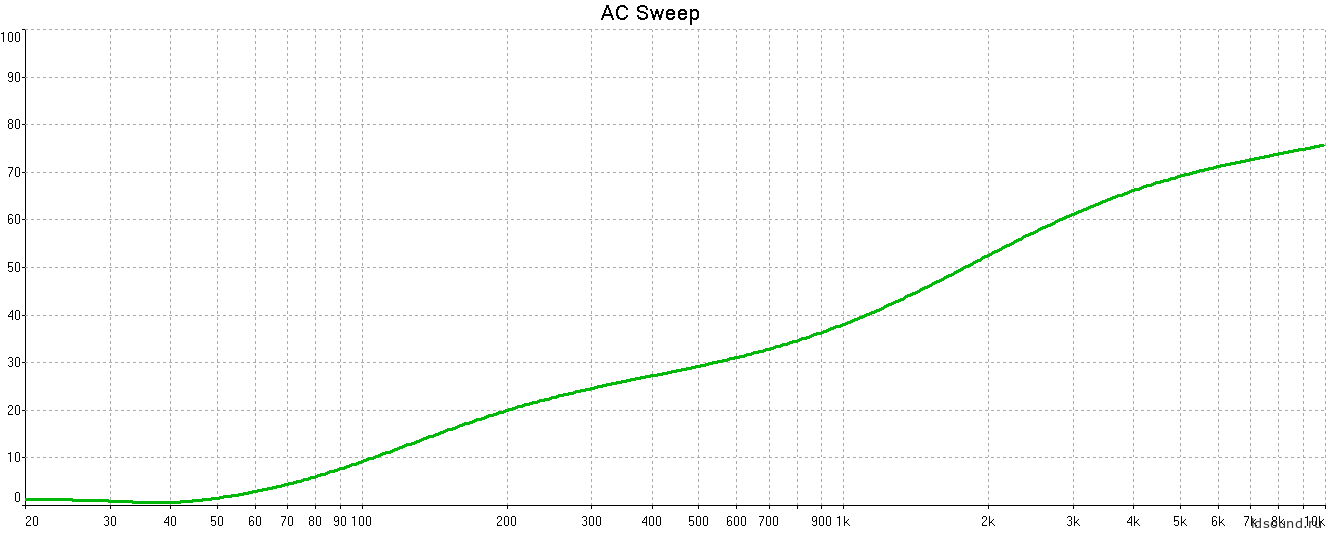
Рис.16 Зависимость ΔI/ΔZзк для динамика 75ГДН-1-4.
НЧ звено от S-90, раздел по -6 дБ на 600 Гц:
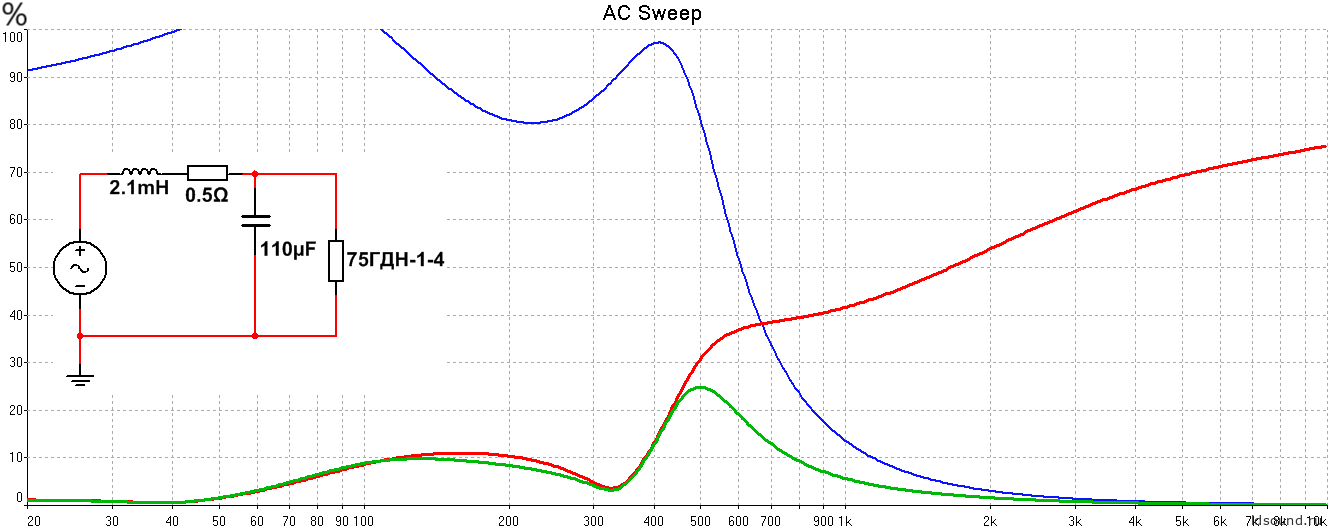
Рис.17 Зависимость ΔI/ΔZзк для популярной схемы.
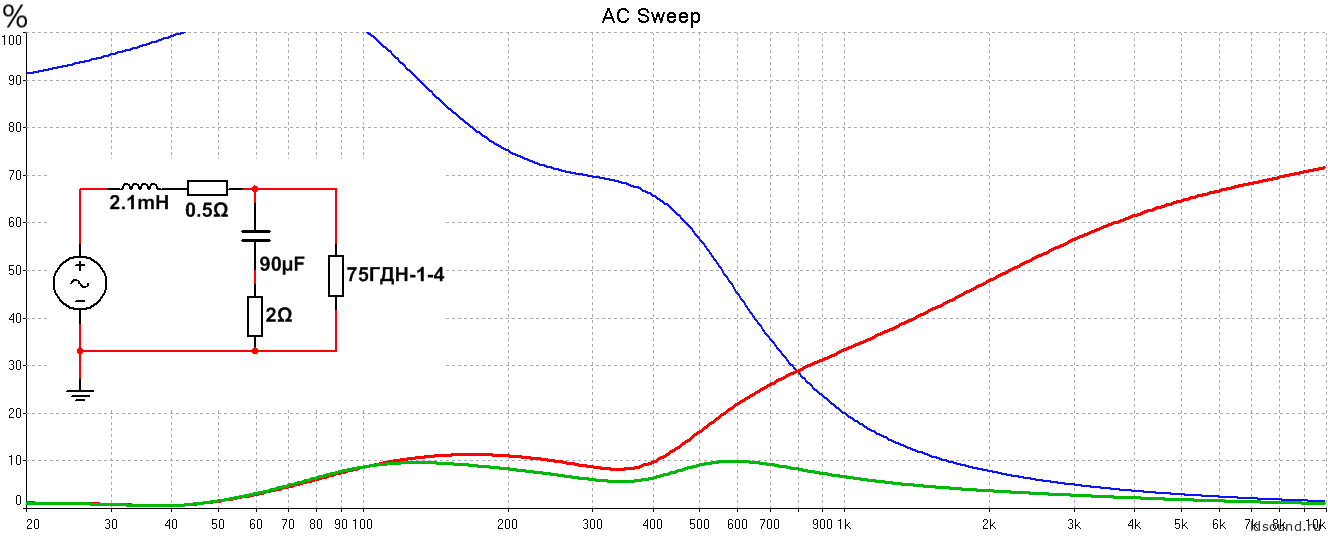
Рис.18 Вариант с «полторашным» ФНЧ, частота раздела по -6 дБ – те же 600 Гц.
Активный ФНЧ второго порядка по Баттерворту с частотой среза по -3 дБ 500 Гц перед УМ с Rвых 22 Ом:
Рис.19 Зависимость ΔI/ΔZзк для наилучшего варианта.
В последнем варианте в тракте должно быть ещё одно звено, уменьшающее коэффициент передачи на СЧ, для компенсации соответствующего подъёма АЧХ: у нас динамик работает от УМ с Rвых 22 Ом, а кривая импеданса 75ГДН задирается уже с 300 Гц. С таким звеном влияние ΔZзк ещё уменьшится выше 300 Гц. Но это всё – сказочки, графики-то мы не слушаем! Расшифрую рис.17, который для фильтра S-90. Если подать на АС S-90 низкочастотный сигнал большой амплитуды, который вызовет изменение импеданса НЧ динамика примерно на -7% на частоте около 4 кГц (требуемая амплитуда смещения диффузора – неизвестна), то сигнал частотой 500 Гц будет амплитудно промодулирован этим низкочастотным сигналом с глубиной 2,5%. Для сравнения – наилучший вариант (рис.19) даст модуляцию меньше 0,5%. Значения – оценочные, глубина модуляции – только за счёт девиации .
И что, гарантировано чистое звучание???
Как бы не так. В формуле (1) есть второй сомножитель – BL. В формуле подразумевается проводник, находящийся в однородном магнитном поле, B = const. На самом деле, у нас ситуация Рис.1: разные витки ЗК находятся в точках пространства с разным значением индукции. Следовательно, BL – величина интегральная:
При смещении ЗК вверх (Рис.1) красных витков становится больше, жёлтых – меньше. Значения индукции в точках, где находятся красные, меньше, чем там, где находятся жёлтые, следовательно, значение интеграла (8) уменьшится. Положение очень напоминает ситуацию с ΔZзк , с той нехорошей разницей, что ΔBL влияет одинаково на всех частотах рабочей полосы, внося как гармонические, так и ИИ. И никаким токовым режимом устранить влияние ΔBL нельзя. Дальше – интереснее. Если бы законы изменения ΔZзк и ΔBL были примерно одинаковы, то их влияния частично компенсировались бы, уменьшая ИИ на средних и/или верхних частотах! В самом деле, поскольку смещению ЗК вверх соответствует уменьшение Zзк (увеличение тока) и уменьшение BL (ослабление мотора), то влияния их изменений на F противоположны по знаку и могли бы частично компенсироваться (о полной компенсации не может быть и речи: ΔZзк – зависит от частоты, а ΔBL – нет). В этом случае токовый режим работы динамика был бы вреден. К сожалению, по зависимостям ΔZзк и ΔBL от смещения диффузора нет никаких данных. Вероятнее всего, законы изменения ΔZзк и ΔBL – разные, и частичной компенсации не будет. Также неясен вопрос о количественном соотношении влияний ΔZзк и ΔBL. Если влияние ΔZзк значительно сильнее, чем ΔBL, то все делаем ИТУН-ы. Если наоборот – закрываем тему токового режима в принципе. Если ΔZзк продуцирует гармоники более высоких порядков, чем ΔBL, делаем ИТУН-ы, если наоборот – закрываем тему… Кулибины-экспериментаторы, ау! Для вас – вариант постановки эксперимента по измерению ИИ. Подаём на подопытный динамик микс из двух частот. Сигнал НЧ должен иметь частоту f1, на которой смещение диффузора максимально, мощность в динамике, скажем, 1/3 номинальной. Второй сигнал – СЧ, с частотой f2, мощность – 1/10 номинальной. Спектроанализатором определяем уровень сигналов с частотой f2 ± f1 (частоты f2 ± 2f1 можно проигнорировать). Повторяем для трёх f2 и трёх значений Rвых = (0…3) · Rном, поддерживая одинаковые уровни мощности сигналов, составляем таблицу. Если с ростом частоты интермодуляционные искажения растут – вклад ΔZзк большой, ИТУН показан. Если не изменяются – ИТУН не поможет, основной вклад даёт ΔBL, возможна частичная компенсация влияний, если уменьшаются – ИТУН вреден. По теории. Отличным, но сложно выполнимым, является тест на сравнение режимов работы на слух на музыке. Для теста необходим комплекс, позволяющий одним щелчком изменять выходное сопротивление УМ, одновременно выравнивая отдачу и АЧХ, и всё это – под каждый конкретный динамик! Не слишком ли много чести?
* * * * *
В результате написания статьи я пришёл к выводу, что предмет темы гораздо менее интересен, чем кажется с наскока. Основное внимание, по моему мнению, следует уделить проблеме минимизации амплитуды смещения диффузора, как первопричине нелинейности (https://ldsound.info/nonlinear-distortion-of-electrodynamic-speakers/). Влияние ΔZзк убирается обычными хорошо продуманными пассивными ФНЧ, а бОльшую нелинейность однозначно даёт ΔBL. И лишь в случае применения широкополосного динамика на весь звуковой диапазон есть смысл опробовать на слух токовый режим работы. Цепочка из параллельно соединённых R и L перед ШП, выравнивающая АЧХ, – приветствуется как увеличивающая выходное сопротивление источника сигнала. Кстати, конструкционные меры, снижающие ΔZзк, снижают и ΔBL. Ищите качественные динамики😊.
* * * * *
Если считать ΔZзк влияние существенным, то:
- Токовый режим работы динамика позволяет исключить один из источников искажений при работе с большим смещением ЗК.
- Разумное проектирование АС позволяет в большинстве случаев сделать то же самое без токового режима.
- Без измерения уровней интермодуляционных искажений или сравнительного прослушивания в двух режимах (ИНУН-ИТУН с коррекцией АЧХ) целесообразность внедрения ИТУН представляется спорной.
Остальные замечания в большей степени относятся к борьбе с ИИ от ΔBL, чем от ΔZзк:
- О высоком качестве двухполосок с частотой раздела выше 3 кГц на базе большинства советских и западных НЧ головок можно говорить лишь при уменьшении мощности подводимого сигнала в разы. При негромком прослушивании будет всё ОК, но номинальную мощность без кучи ИИ получить не удастся. Кстати, уровень ИИ крайне редко измеряется и вообще не регламентируется.
- Частота раздела для 75ГДН при полном использовании по мощности без пассивного ФНЧ должна быть низкой: 200-400 Гц. Для «утюгов» с ещё меньшим отношением Rном/Lзк – и того меньше. (Вспоминаем немцев, рекомендующих делать срез 300 Гц, когда АЧХ «утюга» бежит до 1кГц.)
- «Любимое» значение частоты нижнего раздела 500 Гц продиктовано не только соображениями работы НЧ динамика в поршневом режиме, но и стремлением уменьшить ИИ по причине ΔZзк и ΔBL. Чем уже рабочая полоса частот динамика, болтающегося с большой амплитудой, тем меньше ИИ в звуке.
- Двухполосная АС с частотой раздела 1 кГц и ШП динамиком в ВЧ полосе имеет преимущество перед АС со стандартным высоким разделом (4-5 кГц) при условии, что у ШП динамика нет существенной амплитуды смещения диффузора: ПАС и/или второй порядок обязательны.
Автор: Николай Марков











Николай, как могут быть разные токи в разных участках катушки если все витки в ней включены последовательно?
токами Фуко в катушке можно пренебречь, в медном каркасе они выше
Где я такое вписал? В (8) ток вынесен из-под интеграла. Подскажите, где.
Агеев о токовом режиме работы
https://cxem.net/sound/amps/amp23.php?ysclid=les1xlorva707297129
Отлично. И не лень ведь было пачкать бумагу.
Осталось только применить эти знания на практике, собрать такой динамик. (sarcazm)